Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Walther, Guenther
1997.
Granulometric smoothing.
The Annals of Statistics,
Vol. 25,
Issue. 6,
Bräker, H.
Hsing, T.
and
Bingham, N. H.
1998.
On the Hausdorff distance between a convex set and an interior random convex hull.
Advances in Applied Probability,
Vol. 30,
Issue. 2,
p.
295.
Ba ÍLLO, Amparo
Cuevas, Antonio
and
Justel, Ana
2000.
Set estimation and nonparametric detection.
Canadian Journal of Statistics,
Vol. 28,
Issue. 4,
p.
765.
Baíllo, Amparo
and
Cuevas, Antonio
2001.
On the estimation of a star-shaped set.
Advances in Applied Probability,
Vol. 33,
Issue. 4,
p.
717.
Cuevas, Antonio
and
Rodríguez-Casal, Alberto
2003.
Recent Advances and Trends in Nonparametric Statistics.
p.
251.
Cuevas, Antonio
and
Rodríguez-Casal, Alberto
2004.
On boundary estimation.
Advances in Applied Probability,
Vol. 36,
Issue. 2,
p.
340.
Terán, P.
and
López-Dı́az, M.
2004.
A random approximation of set valued càdlàg functions.
Journal of Mathematical Analysis and Applications,
Vol. 298,
Issue. 1,
p.
352.
Cadre, Benoıˆt
2006.
Kernel estimation of density level sets.
Journal of Multivariate Analysis,
Vol. 97,
Issue. 4,
p.
999.
Cuevas, Antonio
Fraiman, Ricardo
and
Rodríguez-Casal, Alberto
2007.
A nonparametric approach to the estimation of lengths and surface areas.
The Annals of Statistics,
Vol. 35,
Issue. 3,
Mayer, Michael
and
Molchanov, Ilya
2007.
Limit theorems for the diameter of a random sample in the unit ball.
Extremes,
Vol. 10,
Issue. 3,
p.
129.
Pateiro-López, Beatriz
and
Rodríguez-Casal, Alberto
2008.
Length and surface area estimation under smoothness restrictions.
Advances in Applied Probability,
Vol. 40,
Issue. 2,
p.
348.
Carando, Daniel
Fraiman, Ricardo
and
Groisman, Pablo
2009.
Nonparametric likelihood based estimation for a multivariate Lipschitz density.
Journal of Multivariate Analysis,
Vol. 100,
Issue. 5,
p.
981.
Pateiro-López, B.
and
Rodríguez-Casal, A.
2009.
Surface area estimation under convexity type assumptions.
Journal of Nonparametric Statistics,
Vol. 21,
Issue. 6,
p.
729.
Berrendero, José R.
Cuevas, Antonio
and
Pateiro‐López, Beatriz
2012.
Testing uniformity for the case of a planar unknown support.
Canadian Journal of Statistics,
Vol. 40,
Issue. 2,
p.
378.
Cuevas, A.
Fraiman, R.
and
Pateiro-López, B.
2012.
On Statistical Properties of Sets Fulfilling Rolling-Type Conditions.
Advances in Applied Probability,
Vol. 44,
Issue. 2,
p.
311.
Pateiro-López, Beatriz
and
Rodríguez-Casal, Alberto
2013.
Recovering the shape of a point cloud in the plane.
TEST,
Vol. 22,
Issue. 1,
p.
19.
De Vito, Ernesto
Rosasco, Lorenzo
and
Toigo, Alessandro
2014.
Learning sets with separating kernels.
Applied and Computational Harmonic Analysis,
Vol. 37,
Issue. 2,
p.
185.
Rudi, Alessandro
Odone, Francesca
and
De Vito, Ernesto
2014.
Geometrical and computational aspects of Spectral Support Estimation for novelty detection.
Pattern Recognition Letters,
Vol. 36,
Issue. ,
p.
107.
Hug, Daniel
and
Schneider, Rolf
2014.
Approximation Properties of Random Polytopes Associated with Poisson Hyperplane Processes.
Advances in Applied Probability,
Vol. 46,
Issue. 4,
p.
919.
Terán, Pedro
and
López-Díaz, Miguel
2014.
Strong consistency and rates of convergence for a random estimator of a fuzzy set.
Computational Statistics & Data Analysis,
Vol. 77,
Issue. ,
p.
130.


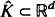 is studied. Basic inequalities are derived for the case of
is studied. Basic inequalities are derived for the case of 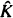 being a convex subset of
being a convex subset of 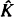 being the intersection of a random family of halfspaces containing
being the intersection of a random family of halfspaces containing 