Consider randomly scattered radio transceivers in ℝd, each of which can transmit signals to all transceivers in a given randomly chosen region about itself. If a signal is retransmitted by every transceiver that receives it, under what circumstances will a signal propagate to a large distance from its starting point? Put more formally, place points {xi} in ℝd according to a Poisson process with intensity 1. Then, independently for each xi, choose a bounded region Axi from some fixed distribution and let 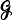be the random directed graph with vertex set 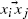whenever xj ∈ xi + Axi. We show that, for any 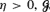will almost surely have an infinite directed path, provided the expected number of transceivers that can receive a signal directly from xi is at least 1 + η, and the regions xi + Axi do not overlap too much (in a sense that we shall make precise). One example where these conditions hold, and so gives rise to percolation, is in ℝd, with each Axi a ball of volume 1 + η centred at xi, where η → 0 as d → ∞. Another example is in two dimensions, where the Axi are sectors of angle ε γ and area 1 + η, uniformly randomly oriented within a fixed angle (1 + ε)θ. In this case we can let η → 0 as ε → 0 and still obtain percolation. The result is already known for the annulus, i.e. that the critical area tends to 1 as the ratio of the radii tends to 1, while it is known to be false for the square (l∞) annulus. Our results show that it does however hold for the randomly oriented square annulus.