We showed in [2] that if an object of initial size x (x large) is subjected to a succession of random partitions, then the object is decomposed into a large number of terminal cells, each of relatively small size, where if Z(x, B) denotes the number of such cells whose sizes are points in the set B, then there exists c, (0 < ≦ 1), such that Z(x, B)x−c converges in probability, as x → ∞, to a random variable W. We show here that if a parent object of size x produces k offspring of sizes y1, y2, ···, yk and if for each k x - y1 - y2 - ··· - yk (the ‘waste’ or the ‘cover’, depending on the point of view) is relatively small, then for each n the nth cumulant, Ψn (x, B), of Z(x, B) satisfies Ψn (x, B)x-c → κn (B), as x → ∞, for some κn(B). Thus, writing N = xc, Z(x, B) has approximately the same distribution as the sum of N independent and identically distributed random variables 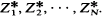(The determination of the distribution of the individual 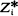appears to be a difficult problem.) The theory also applies when an object of moderate size is broken down into very fine particles or granules.