Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T10:53:15.614Z Has data issue: false hasContentIssue false
  • English
  • Français

Random Marked Sets

Part of: Stochastic processes Geometric probability and stochastic geometry

Published online by Cambridge University Press:  04 January 2016

F. Ballani ,
Z. Kabluchko  and
M. Schlather
F. Ballani*
Affiliation:
TU Bergakademie Freiberg
Z. Kabluchko*
Affiliation:
Universität Ulm
M. Schlather*
Affiliation:
Universität Göttingen
*
∗ Postal address: Institut für Stochastik, TU Bergakademie Freiberg, D-09596 Freiberg, Germany. Email address: [email protected]
∗∗ Postal address: Institut für Stochastik, Universität Ulm, Helmholtzstr. 18, D-89069 Ulm, Germany. Email address: [email protected]
∗∗∗ Current address: Institut für Mathematik, Universität Mannheim, A5, 6, D-68131 Mannheim, Germany. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

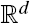We aim to link random fields and marked point processes, and, therefore, introduce a new class of stochastic processes which are defined on a random set in . Unlike for random fields, the mark covariance function of a random marked set is in general not positive definite. This implies that in many situations the use of simple geostatistical methods appears to be questionable. Surprisingly, for a special class of processes based on Gaussian random fields, we do have positive definiteness for the corresponding mark covariance function and mark correlation function.

Keywords

Random fieldrandom setmarked point processmark correlation functionmark covariance function

MSC classification

Primary: 60G60: Random fields 60G55: Point processes
Secondary: 60G15: Gaussian processes 60D05: Geometric probability and stochastic geometry
Type
Stochastic Geometry and Statistical Applications
Information
Advances in Applied Probability , Volume 44 , Issue 3 , September 2012 , pp. 603 - 616
Copyright
© Applied Probability Trust 

References

Adler, R. J. (1981). The Geometry of Random Fields. John Wiley, Chichester.Google Scholar
Adler, R. J. and Taylor, J. E. (2007). Random Fields and Geometry. Springer, New York.Google Scholar
Ballani, F., Kabluchko, Z. and Schlather, M. (2012). Random marked sets. Preprint. Available at http://arxiv.org/abs/0903.2388v2.Google Scholar
Beneš, V. and Rataj, J. (2004). Stochastic Geometry: Selected Topics. Kluwer, Boston, MA.Google Scholar
Cramér, H. and Leadbetter, M. R. (1967). Stationary and Related Stochastic Processes. Sample Function Properties and Their Applications. John Wiley, New York.Google Scholar
Cressie, N. A. C. (1993). Statistics for Spatial Data. John Wiley, New York.Google Scholar
Cressie, N., Frey, J., Harch, B. and Smith, M. (2006). Spatial prediction on a river network. J. Agricultural Biol. Environ. Statist., 11, 127–150.Google Scholar
Daley, D. J. and Vere-Jones, D. (2008). An Introduction to the Theory of Point Processes, Vol. II. Springer, New York.Google Scholar
Diggle, P. J., Menezes, R. and Su, T.-L. (2010). Geostatistical inference under preferential sampling. J. R. Statist. Soc. C 59, 191–232.Google Scholar
Diggle, P. J., Ribeiro, P. J. Jr. and Christensen, O. F. (2003). An introduction to model-based geostatistics. In Spatial Statistics and Computational Methods (Aalborg, 2001; Lecture Notes Statist. 173), ed. Møller, J., Springer, New York, pp. 43–86.CrossRefGoogle Scholar
Guan, Y., Sherman, M. and Calvin, J. A. (2004). A nonparametric test for spatial isotropy using subsampling. J. Amer. Statist. Assoc. 99, 810–821.Google Scholar
Hug, D., Last, G. and Weil, W. (2004). A local Steiner-type formula for general closed sets and applications. Math. Z. 246, 237–272.Google Scholar
Illian, J., Penttinen, A., Stoyan, H. and Stoyan, D. (2008). Statistical Analysis and Modelling of Spatial Point Patterns. John Wiley, Chichester.Google Scholar
Kangas, A. and Maltamo, M. (2006). Forest Inventory: Methodology and Applications. Springer, Dordrecht.CrossRefGoogle Scholar
Kraynik, A. M. (1988). Foam flows. Ann. Rev. Fluid Mech. 20, 325–357.Google Scholar
Liski, J. and Westman, C. J. (1997). Carbon storage in forest soil of Finland. Biogeochemistry 36, 239–260.Google Scholar
Matheron, G. (1969). Théorie des ensembles aléatoires. In Les Cahiers du Centre Morphologie Mathematique de Fontainebleau, Fasc. 4, Ecole des Mines de Paris.Google Scholar
Matheron, G. (1975). Random Sets and Integral Geometry. John Wiley, New York.Google Scholar
Molchanov, I. (1983). Labelled random sets. Teor. Veroyat. Matem. Statist. 29, 93–98 (in Russian). English translation: Theory Prob. Math. Statist. 29 (1984), 113-119.Google Scholar
Molchanov, I. (2005). Theory of Random Sets. Springer, London.Google Scholar
Pólya, G. (1949). Remarks on characteristic functions. In Proc. Berkeley Symp. on Mathematical Statistics and Probability, ed. Neyman, J., University of California Press, pp. 115–123.Google Scholar
Sasvári, Z. (1994). Positive Definite and Definitizable Functions. Akademie, Berlin.Google Scholar
Schlather, M. (2001). On the second-order characteristics of marked point processes. Bernoulli 7, 99–117.Google Scholar
Schlather, M., Ribeiro, P. J. Jr. and Diggle, P. J. (2004). Detecting dependence between marks and locations of marked point processes. J. R. Statist. Soc. B 66, 79–93.CrossRefGoogle Scholar
Serra, J. (1982). Image Analysis and Mathematical Morphology. Academic Press, London.Google Scholar
Stoyan, D., Kendall, W. S. and Mecke, J. (1995). Stochastic Geometry and Its Applications. John Wiley, Chichester.Google Scholar
Takahata, H. (1994). Nonparametric density estimation for a class of marked point processes. Yokohama Math. J. 41, 127–152.Google Scholar
Wälder, O. and Stoyan, D. (1996). On variograms in point process statistics. Biometrical J. 38, 895–905.CrossRefGoogle Scholar
Wallerman, J., Joyce, S., Vencatasawmy, C. P. and Olsson, H. (2002). Prediction of forest stem volume using kriging adapted to detected edges. Canad. J. Forest Res. 32, 509–518.CrossRefGoogle Scholar