Hostname: page-component-6bf8c574d5-9nwgx Total loading time: 0 Render date: 2025-02-19T22:17:40.028Z Has data issue: false hasContentIssue false
  • English
  • Français

Quadratic transformations: a model for population growth. II

Published online by Cambridge University Press:  01 July 2016

Harry Kesten
Harry Kesten*
Affiliation:
Cornell University
Get access Rights & Permissions [Opens in a new window]

Extract

In this last part the Fn(i) and Mn(i) are considered as random variables whose distributions are described by the model and various mating rules of Section 2. Several convergence results will be proved for those specific mating rules, but we begin with the more general convergence theorem 6.1. The proof of this theorem brings out the basic idea of this section, namely that when Fn and Mn are large, Fn + 1(i) and Mn + 1(i) will, with high probability, be close to a certain function of Fn(·) and Mn(·) (roughly the conditional expectation of Fn+1(i) and Mn + 1(i) given Fn(·) and Mn(·)). 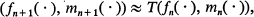As we already indicated in Section 2, this leads (outside the exceptional set) to the approximate equality for some transformation T of the form (1.4), (1.5). More generally for fixed k 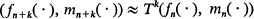except on a set whose probability is small when Fn and Mn are large. If the theorems of Section 3 or 4 apply, Tk(fn(·), mn(·)) will be close to a fixed vector ζ when k is large and thus there is hope that fn(·) and mn(·) will converge, once Fn and Mn become large. We therefore have to put on some conditions which will make Fn and Mn grow. This is the role of (6.34) and, to some extent, also of (6.17). The main difficulty is that the expected size of the (n + 1)th generation, given the nth generation, depends on the frequencies of the different types present in the nth generation. Even if (6.34) holds, the conditional expected size of the (n + 1)th generation, given the nth generation, may actually be smaller than the size of the nth generation for certain directions fn(·), m(·).

Type
Research Article
Information
Advances in Applied Probability , Volume 2 , Issue 2 , Autumn 1970 , pp. 179 - 228
Copyright
Copyright © Applied Probability Trust 1970 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bharucha-Reid, A. T. (1960) Elements of the Theory of Markov Processes and Their Applications. McGraw-Hill, New York.Google Scholar
Blakley, G. R. (1964) The sequence of iterates of a nonnegative nonlinear transformation I. Preprint. (See also Bull. Amer. Math. Soc. 70, 712–715 and an article with Dixon, R. D.: The iterates of a homogeneous symmetric quadratic transformation. To appear in J. Stat. Physics (1969).) Google Scholar
Blakley, G. R. and Dixon, R. D. (1964) The sequence of iterates of a nonnegative nonlinear transformation II and III. Preprint.Google Scholar
Bodmer, W. F. (1960) Discrete stochastic processes in population genetics. J. R. Statist. Soc. B 22, 218–244.Google Scholar
Bodmer, W. F. (1965) Differential fertility in population genetics models. Genetics 51, 411–424.Google Scholar
Bodmer, W. F. and Parsons, P. A. (1962) Linkage and recombination in evolution. Advances in Genetics 11, 1–100.Google Scholar
Breiman, L. (1968) Probability. Addison-Wesley Publ. Co., Reading, Mass.Google Scholar
Cesari, L. (1959) Asymptotic Behavior and Stability Problems in Ordinary Differential Equations. Springer Verlag, Berlin.Google Scholar
Coddington, E. A. and Levinson, N. (1955) Theory of Ordinary Differential Equations. McGraw-Hill, New York.Google Scholar
Daley, D. J. (1968) Extinction conditions for certain bisexual Galton-Watson processes. Z. Wahrscheinlichkeitsth. 9, 315–322.Google Scholar
Dobrushin, R. L. (1956) Central limit theorem for nonstationary Markov chains II. Teor. Veroyat. Primen. 1, 365–425 (translated in Theor. Probability Appl. 1, 329–383).Google Scholar
Doob, J. L. (1953) Stochastic Processes. John Wiley & Sons, Inc., New York.Google Scholar
Dubins, L. E. and Freedman, D. A. (1965) A sharper form of the Borel-Cantelli lemma and the strong law. Ann. Math. Statist. 36, 800–807.CrossRefGoogle Scholar
Dugundji, J. (1966) Topology. Allyn & Bacon, Inc., Boston.Google Scholar
Ellison, B. E. (1966) Limit theorems for random mating in infinite populations. J. Appl. Prob. 3, 94–144.Google Scholar
Feller, W. (1951) Diffusion processes in genetics. Proc. Second Berkeley Symp. on Math. Stat. and Prob. 227–246.Google Scholar
Feller, W. (1968) An Introduction to Probability Theory and its Applications. Vol. 1, 3rd ed. John Wiley & Sons, Inc., New York.Google Scholar
Fisher, R. A. (1930) The Genetical Theory of Natural Selection. Clarendon Press, Oxford.Google Scholar
Fisher, R. A. (1941–1942) Average excess and average effect of a gene substitution. Ann. Eugen. 11, 53–63.Google Scholar
Fréchet, M. (1938) Recherches théoriques modernes sur le calcul des probabilités, II. Méthode des fonctions arbitraires. Théorie des événements en chaîne dans le cas d'un nombre fini d'états possibles. Note A, 256–273. Gauthier-Villars, Paris.Google Scholar
Gantmacher, F. R. (1959) The Theory of Matrices. Chelsea Publ. Co., New York.Google Scholar
Geiringer, H. (1948) On the mathematics of random mating in case of different recombination values for males and females. Genetics 33, 548–564.Google Scholar
Geiringer, H. (1949 a) On some mathematical problems arising in the development of Mendelian genetics. J. Amer. Statist. Ass. 44, 526–547.Google Scholar
Geiringer, H. (1949 b) Chromatid segregation of tetraploids and hexaploids. Genetics 34, 665–684.Google Scholar
Hajnal, J. (1958) Weak ergodicity in non-homogeneous Markov chains. Proc. Camb. Phil. Soc. 54, 233–246.Google Scholar
Haldane, J. B. S. (1932) Appendix to “The Causes of Evolution”. Harper & Brothers, London.Google Scholar
Haldane, J. B. S. (1941–1942) Selection against heterozygosis in man. Ann. Eugen. 11, 333–340.Google Scholar
Harris, T. E. (1963) The Theory of Branching Processes. Springer Verlag, Berlin.Google Scholar
Holgate, P. (1966) A mathematical study of the founder principle of evolutionary genetics. J. Appl. Prob. 3, 115–128.Google Scholar
Hopf, E. (1963) An inequality for positive linear integral operators. J. Math. Mech. 12, 683–692.Google Scholar
Jenks, R. D. (1968) Homogeneous multidimensional differential systems for mathematical models. J. Differential Equations 4, 549–565.Google Scholar
Jenks, R. D. (1969) Quadratic differential systems for mathematical models. Appl. Math. Dept. Report, Brookhaven Nat. Lab. Partially in J. Differential Equations 5, 497–514.Google Scholar
Karlin, S. (1962–1963) Lectures on mathematical biology. Stanford University.Google Scholar
Karlin, S. (1968) Equilibrium behavior of population genetic models with non-random mating. J. Appl. Prob. 5, 231–313 and 487–566.Google Scholar
Karlin, S. and Feldman, M. W. (1968 a) Analysis of models with homozygote and heterozygote matings. Genetics 59, 105–116.Google Scholar
Karlin, S. and Feldman, M. W. (1968 b) Further analysis of negative assortative mating. Genetics 59, 117–136.Google Scholar
Karlin, S. and Feldman, M. W. (1969) Linkage and selection: new equilibrium properties of the two-locus symmetric viability model. Proc. Nat. Acad. Sci. 62, 70–74.Google Scholar
Kempthorne, O. (1957) An Introduction to Genetic Statistics. John Wiley & Sons, Inc., New York.Google Scholar
Kesten, H. and Stigum, B. P. (1966 a) A limit theorem for multi-dimensional Galton-Watson processes. Ann. Math. Statist. 37, 1211–1223.Google Scholar
Kesten, H. and Stigum, B. P. (1966 b) Additional limit theorems for indecomposable multi-dimensional Galton-Watson processes. Ann. Math. Statist. 37, 1463–1481.Google Scholar
Kesten, H. and Stigum, B. P. (1967) Limit theorems for decomposable multi-dimensional Galton-Watson processes. J. Math. Anal. Appl. 17, 309–338.Google Scholar
Kimura, M. (1956) A model of a genetic system which leads to closer linkage by natural selection. Evolution 10, 278–287.Google Scholar
Kimura, M. (1958) On the change of population fitness by natural selection. Heredity 12, 145–167.Google Scholar
Lewontin, R. C. and Kojima, K. (1960) The evolutionary dynamics of complex polymorphisms. Evolution 14, 458–472.Google Scholar
Li, C. C. (1955) Population Genetics. Univ. of Chicago Press, Chicago.Google Scholar
Li, C. C. (1967) Genetic equilibrium under selection. Biometrics 23, 397–484.Google Scholar
Lynn, M. S. and Timlake, W. P. (1967) Bounds for Perron eigenvectors and subdominant eigenvalues of positive matrices. Notices Amer. Math. Soc. 14, 516, Abstract 67T–329.Google Scholar
Menzel, M. T., Stein, P. R. and Ulam, S. M. (1959) Quadratic transformations I. Report LA 2305, Los Alamos Scientific Laboratory, Los Alamos, N.M. Google Scholar
Moran, P. A. P. (1962) The Statistical Processes of Evolutionary Theory. Clarendon Press, Oxford.Google Scholar
Moran, P. A. P. (1964) The non-existence of adaptive topographies. Ann. Hum. Genet. 27, 383–393.Google Scholar
Moran, P. A. P. (1965) Unsolved problems in evolutionary theory. Proc. Fifth Berkeley Symp. on Math. Stat. and Prob. IV. 457–480.Google Scholar
Moran, P. A. P. (1968) On the theory of selection dependent on two loci. Ann. Hum. Genet. 32, 183–190.Google Scholar
Mulholland, H. P. and Smith, C. A. B. (1959) An inequality arising in genetical theory. Amer. Math. Monthly 66, 673–683.Google Scholar
Norton, H. T. J. (1928) Natural selection and Mendelian variation. Proc. Lond. Math. Soc. 2, 28, 1–45.CrossRefGoogle Scholar
Ostrowski, A. M. (1963) On positive matrices. Math. Ann. 150, 276–284.Google Scholar
Ostrowski, A. M. (1966) Solutions, of Equations and Systems of Equations. 2nd ed. Academic Press, New York.Google Scholar
Owen, A. R. G. (1953) A genetical system admitting of two distinct stable equilibria under natural selection. Heredity 7, 97–102.Google Scholar
Parsons, P. A. (1959) Equilibria in auto-tetraploids under natural selection for a simplified model of viabilities. Biometrics 15, 20–29.Google Scholar
Parsons, P. A. (1963 a) Polymorphism and the balanced polygenic combination. Evolution 17, 564–574.Google Scholar
Parsons, P. A. (1963 b) Complex polymorphisms where the coupling and repulsion heterozygotes differ. Heredity 18, 369–374.Google Scholar
Parsons, P. A. (1964) Polymorphism and the balanced polygenic complex — a comment. Evolution, 18, 512.Google Scholar
Prout, T. (1968) A model for the study of mating interactons. Dept. of Genetics Report, Aarhus Universitet.Google Scholar
Reiersöl, O. (1962) Genetic algebras studied recursively and by means of differential operators. Math. Scand. 10, 25–44.Google Scholar
Singer, K. (1953) Application of the theory of stochastic processes to the study of irreproducible chemical reactions and nucleation processes. J. R. Statist. Soc. B 15, 92–106.Google Scholar
Sinnott, E. W., Dunn, L. C. and Dobzhansky, T. (1958) Principles of Genetics. 5th ed. McGraw Hill Book Co., Inc., New York.Google Scholar
Stein, P. R. and Ulam, S. M. (1964) Non-linear transformation studies on electronic computers. Rozprawy Mat. 39.Google Scholar
Ueno, T. (1958) Some limit theorems for temporally discrete Markov processes II. J. Fac. Sci. Univ. Tokyo Sect. I, 7 (5), 557–565.Google Scholar
Wright, S. (1931) Evolution in Mendelian populations. Genetics 16, 97–159.Google Scholar