Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Piterbarg, V. I.
1983.
Gaussian stochastic processes.
Journal of Soviet Mathematics,
Vol. 23,
Issue. 5,
p.
2599.
Wilson, Richard J.
1988.
Model fields in crossing theory: a weak convergence perspective.
Advances in Applied Probability,
Vol. 20,
Issue. 4,
p.
756.
Beckman, Stig‐Inge
Holst, Jan
and
Lindgren, Georg
1990.
ALARM CHARACTERISTICS FOR A FLOOD WARNING SYSTEM WITH DETERMINISTIC COMPONENTS.
Journal of Time Series Analysis,
Vol. 11,
Issue. 1,
p.
1.
Haimes, Yacov Y.
Li, Duan
and
Stakhiv, Eugene Z.
1991.
Water Resources Engineering Risk Assessment.
p.
337.
Bakker, G.J.
and
Blom, H.A.P.
1993.
Air traffic collision risk modelling.
p.
1464.
Gadrich, Tamar
and
Adler, Robert J.
1993.
Slepian models for non-stationary Gaussian processes.
Journal of Applied Probability,
Vol. 30,
Issue. 01,
p.
98.
Lindgren, Georg
and
Eriksson, Weine
1994.
Clicks in Zero-Crossing-Detecting FM Receivers: Theory and Experiments.
Probability in the Engineering and Informational Sciences,
Vol. 8,
Issue. 2,
p.
265.
Blanke, Delphine
and
Vial, Céline
2006.
Estimation du nombre de dérivées d'un processus Gaussien.
Comptes Rendus. Mathématique,
Vol. 343,
Issue. 10,
p.
661.
Blanke, Delphine
and
Vial, Céline
2008.
Assessing the number of mean square derivatives of a Gaussian process.
Stochastic Processes and their Applications,
Vol. 118,
Issue. 10,
p.
1852.
Blanke, Delphine
and
Vial, Céline
2011.
Estimating the order of mean-square derivatives with quadratic variations.
Statistical Inference for Stochastic Processes,
Vol. 14,
Issue. 1,
p.
85.
Liu, Jingchen
and
Xu, Gongjun
2014.
On the conditional distributions and the efficient simulations of exponential integrals of Gaussian random fields.
The Annals of Applied Probability,
Vol. 24,
Issue. 4,
Blanke, Delphine
and
Vial, Céline
2014.
Global smoothness estimation of a Gaussian process from general sequence designs.
Electronic Journal of Statistics,
Vol. 8,
Issue. 1,
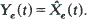 An example of this is the prediction of water level near a coast, when A(t) is a sum of known tide components.
An example of this is the prediction of water level near a coast, when A(t) is a sum of known tide components.