Published online by Cambridge University Press: 16 January 2023
Given a spectrally negative Lévy process, we predict, in an
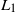 $L_1$
sense, the last passage time of the process below zero before an independent exponential time. This optimal prediction problem generalises [2], where the infinite-horizon problem is solved. Using a similar argument as that in [24], we show that this optimal prediction problem is equivalent to solving an optimal prediction problem in a finite-horizon setting. Surprisingly (unlike the infinite-horizon problem), an optimal stopping time is based on a curve that is killed at the moment the mean of the exponential time is reached. That is, an optimal stopping time is the first time the process crosses above a non-negative, continuous, and non-increasing curve depending on time. This curve and the value function are characterised as a solution of a system of nonlinear integral equations which can be understood as a generalisation of the free boundary equations (see e.g. [21, Chapter IV.14.1]) in the presence of jumps. As an example, we numerically calculate this curve in the Brownian motion case and for a compound Poisson process with exponential-sized jumps perturbed by a Brownian motion.
$L_1$
sense, the last passage time of the process below zero before an independent exponential time. This optimal prediction problem generalises [2], where the infinite-horizon problem is solved. Using a similar argument as that in [24], we show that this optimal prediction problem is equivalent to solving an optimal prediction problem in a finite-horizon setting. Surprisingly (unlike the infinite-horizon problem), an optimal stopping time is based on a curve that is killed at the moment the mean of the exponential time is reached. That is, an optimal stopping time is the first time the process crosses above a non-negative, continuous, and non-increasing curve depending on time. This curve and the value function are characterised as a solution of a system of nonlinear integral equations which can be understood as a generalisation of the free boundary equations (see e.g. [21, Chapter IV.14.1]) in the presence of jumps. As an example, we numerically calculate this curve in the Brownian motion case and for a compound Poisson process with exponential-sized jumps perturbed by a Brownian motion.