Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-23T05:06:28.663Z Has data issue: false hasContentIssue false
  • English
  • Français

Poisson approximation for some statistics based on exchangeable trials

Published online by Cambridge University Press:  01 July 2016

A. D. Barbour  and
G. K. Eagleson
A. D. Barbour*
Affiliation:
Gonville and Caius College, Cambridge
G. K. Eagleson*
Affiliation:
CSIRO Division of Mathematics and Statistics
*
∗Present address: Institut für Angewandte Mathematik, Universität Zürich, Rämistrasse 74, CH-8001 Zürich, Switzerland.
∗∗Postal address: CSIRO Division of Mathematics and Statistics, Bradfield Rd, West Lindfield, NSW 2070, Australia.
Get access Rights & Permissions [Opens in a new window]

Abstract

Stein's (1970) method of proving limit theorems for sums of dependent random variables is used to derive Poisson approximations for a class of statistics, constructed from finitely exchangeable random variables.

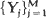Let be exchangeable random elements of a space 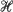and, for I a k-subset of 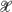, let XI be a 0–1 function. The statistics studied here are of the form 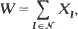where N is some collection of k -subsets of .

An estimate of the total variation distance between the distributions of W and an appropriate Poisson random variable is derived and is used to give conditions sufficient for W to be asymptotically Poisson. Two applications of these results are presented.

Keywords

FINITELY EXCHANGEABLE RANDOM VARIABLES
Type
Research Article
Information
Advances in Applied Probability , Volume 15 , Issue 3 , September 1983 , pp. 585 - 600
Copyright
Copyright © Applied Probability Trust 1983 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barton, D. E. and David, F. N. (1966) The random intersection of two graphs. In Research Papers in Statistics, ed. David, F. N., Wiley, New York, 445–459.Google Scholar
Berman, M. and Eagleson, G. K. (1983) A Poisson limit theorem for incomplete symmetric statistics. J. Appl. Prob. 20, 47–60.Google Scholar
Brown, T. C. (1981) Compensators and Cox convergence. Math. Proc. Camb. Phil. Soc. 90, 305–319.Google Scholar
Brown, T. C. and Silverman, B. S. (1979) Rates of Poisson convergence for U-statistics. J. Appl. Prob. 16, 428–432.Google Scholar
Chen, L. H. Y. (1975) Poisson approximation for dependent trials. Ann. Prob. 3, 534–545.Google Scholar
Eagleson, G. K. (1979) A Poisson limit theorem for weakly exchangeable arrays. J. Appl. Prob. 16, 794–802.Google Scholar
Knox, G. (1964) Epidemiology of childhood leukaemia in Northumberland and Durham. Brit. J. Prev. Soc. Med. 18, 17–24.Google ScholarPubMed
Silverman, B. S. and Brown, T. C. (1978) Short distances, flat triangles and Poisson limits. J. Appl. Prob. 15, 815–825.CrossRefGoogle Scholar
Stein, C. (1970) A bound for the error in the normal approximation to the distribution of a sum of dependent random variables. Proc. 6th Berkeley Symp. Math. Statist. Prob. 2, 583–602.Google Scholar