Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T15:23:01.512Z Has data issue: false hasContentIssue false
  • English
  • Français

Percolation and Connectivity in AB Random Geometric Graphs

Part of: Graph theory Geometric probability and stochastic geometry Equilibrium statistical mechanics

Published online by Cambridge University Press:  04 January 2016

Srikanth K. Iyer  and
D. Yogeshwaran
Srikanth K. Iyer*
Affiliation:
Indian Institute of Science
D. Yogeshwaran*
Affiliation:
INRIA/ENS
*
∗ Postal address: Department of Mathematics, Indian Institute of Science, Bangalore 560012, India. Email address: [email protected]
∗∗ Current address: Faculty of Electrical Engineering, Technion, Israel Institute of Technology, Haifa, 32000, Israel.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given two independent Poisson point processes Φ(1), Φ(2) in 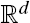, the AB Poisson Boolean model is the graph with the points of Φ(1) as vertices and with edges between any pair of points for which the intersection of balls of radius 2r centered at these points contains at least one point of Φ(2). This is a generalization of the AB percolation model on discrete lattices. We show the existence of percolation for all d ≥ 2 and derive bounds for a critical intensity. We also provide a characterization for this critical intensity when d = 2. To study the connectivity problem, we consider independent Poisson point processes of intensities n and τn in the unit cube. The AB random geometric graph is defined as above but with balls of radius r. We derive a weak law result for the largest nearest-neighbor distance and almost-sure asymptotic bounds for the connectivity threshold.

Keywords

Random geometric graphpercolationconnectivitywireless networksecure communication

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry 05C80: Random graphs
Secondary: 82B43: Percolation 05C40: Connectivity
Type
Stochastic Geometry and Statistical Applications
Information
Advances in Applied Probability , Volume 44 , Issue 1 , March 2012 , pp. 21 - 41
Copyright
© Applied Probability Trust 

Footnotes

Research supported in part by UGC SAP-IV and DRDO, grant no. DRDO/PAM/SKI/593.

Supported in part by a grant from EADS, France, Israel Science foundation (grant no. 853/10), and AFOSR (grant no. FA8655-11-1-3039).

References

Appel, M. J. and Wierman, J. C. (1987). On the absence of infinite AB percolation clusters in bipartite graphs. J. Phys. A 20, 2527–2531.CrossRefGoogle Scholar
Benjamini, I. and Kesten, H. (1995). Percolation of arbitrary words in 0,1 mN . Ann. Prob. 23, 1024–1060.Google Scholar
Dousse, O. et al. (2006). Percolation in the signal to interference ratio graph. J. Appl. Prob. 43, 552–562.Google Scholar
Franceschetti, M., Dousse, O., Tse, D. N. C. and Thiran, P. (2007). Closing the gap in the capacity of wireless networks via percolation theory. IEEE Trans. Inf. Theory 53, 1009–1018.Google Scholar
Gilbert, E. N. (1961). Random plane networks. J. Soc. Indust. Appl. Math. 9, 533–543.Google Scholar
Goldstein, L. and Penrose, M. D. (2010). Normal approximation for coverage models over binomial point processes. Ann. Appl. Prob. 20, 696–721.Google Scholar
Grimmett, G. (1999). Percolation. Springer, Berlin.Google Scholar
Gupta, P. and Kumar, P. R. (2000). The capacity of wireless networks. IEEE Trans. Inf. Theory 46, 388–404.Google Scholar
Haenggi, M. (2008). The secrecy graph and some of its properties. In Proc. IEEE Internat. Symp. Inf. Theory (Toronto, 2008).Google Scholar
Hall, P. (1988). Introduction to the Theory of Coverage Processes. John Wiley, New York.Google Scholar
Halley, J. W. (1980). AB percolation on triangular lattice. In Ordering in Two Dimensions, ed. Sinha, S., North-Holland, Amsterdam, pp. 369–371.Google Scholar
Halley, J. W. (1983). Polychromatic percolation. In Percolation Structures and Processes, eds Deutscher, G., Zallen, R. and Adler, J., Israel Physical Society, pp. 323–351.Google Scholar
Kesten, H., Sidoravicius, V. and Zhang, Y. (1998). Almost all words are seen at critical site percolation on the triangular lattice. Electron. J. Prob. 4, 75pp.Google Scholar
Kesten, H., Sidoravicius, V. and Zhang, Y. (2001). Percolation of arbitrary words on the close-packed graph of Z2 . Electron. J. Prob. 6, 27pp.Google Scholar
Meester, R. and Roy, R. (1996). Continuum Percolation. Cambridge University Press.Google Scholar
Moran, P. A. P. (1973). The random volume of interpenetrating spheres in space. J. Appl. Prob. 10, 483–490.CrossRefGoogle Scholar
Penrose, M. (2003). Random Geometric Graphs. Oxford University Press.Google Scholar
Pinto, P. C. and Win, M. Z. (2010). Percolation and connectivity in the intrinsically secure communications graph. Preprint. Available at http://arxiv.org/abs/1008.4161v1.Google Scholar
Scheinerman, E. R. and Wierman, J. C. (1987). Infinite AB clusters exist. J. Phys. A 20, 1305–1307.CrossRefGoogle Scholar
Sevšek, F., Debierre, J.-M. and Turban, L. (1983). Antipercolation on Bethe and triangular lattices. J. Phys. A 16, 801–810.Google Scholar
Tanemura, H. (1996). Critical behaviour for a continuum percolation model. In Probability Theory and Mathematical Statistics (Tokyo, 1995), eds Watanabe, S. et al., World Scientific, River Edge, NJ, pp. 485–495.Google Scholar
Tse, D. and Vishwanath, P. (2005). Fundamentals of Wireless Communication. Cambridge University Press.Google Scholar
Wierman, J. C. and Appel, M. J. (1987). Infinite AB percolation clusters exist on the triangular lattice. J. Phys. A 20, 2533–2537.Google Scholar
Wu, X.-Y. and Popov, S. Y. (2003). On AB bond percolation on the square lattice and AB site percolation on its line graph. J. Statist. Phys. 110, 443–449.Google Scholar