Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fagiuoli, E.
and
Pellerey, F.
1994.
Mean residual life and increasing convex comparison of shock models.
Statistics & Probability Letters,
Vol. 20,
Issue. 5,
p.
337.
Kebir, Y.
1994.
Order-Preserving Shock Models.
Probability in the Engineering and Informational Sciences,
Vol. 8,
Issue. 1,
p.
125.
Shaked, Moshe
and
Wong, Tityik
1995.
Preservation of Stochastic Orderings under Random Mapping by Point Processes.
Probability in the Engineering and Informational Sciences,
Vol. 9,
Issue. 4,
p.
563.
Di Crescenzo, Antonio
and
Ricciardi, Luigi M
1996.
Comparing first-passage times for semi-Markov skip-free processes.
Statistics & Probability Letters,
Vol. 30,
Issue. 3,
p.
247.
Lynch, James D.
1997.
When Is a Renewal Process Convexly Parameterized in Its Mean Parameterization?.
Probability in the Engineering and Informational Sciences,
Vol. 11,
Issue. 1,
p.
43.
Shaked, Moshe
and
Wong, Tityik
1997.
Stochastic orders based on ratios of Laplace transforms.
Journal of Applied Probability,
Vol. 34,
Issue. 02,
p.
404.
Wong, Tityik
1997.
Preservation of multivariate stochastic orders under multivariate Poisson shock models.
Journal of Applied Probability,
Vol. 34,
Issue. 04,
p.
1009.
Pellerey, Franco
1999.
Stochastic Comparisons for Multivariate Shock Models.
Journal of Multivariate Analysis,
Vol. 71,
Issue. 1,
p.
42.
Belzunce, Félix
Ortega, Eva
and
Ruiz, José M.
1999.
The Laplace order and ordering of residual lives.
Statistics & Probability Letters,
Vol. 42,
Issue. 2,
p.
145.
Ebrahimi, Nader
1999.
Stochastic properties of a cumulative damage threshold crossing model.
Journal of Applied Probability,
Vol. 36,
Issue. 3,
p.
720.
Ebrahimi, Nader
1999.
Stochastic properties of a cumulative damage threshold crossing model.
Journal of Applied Probability,
Vol. 36,
Issue. 03,
p.
720.
Scarsini, Marco
and
Shaked, Moshe
2000.
On the value of an item subject to general repair or maintenance.
European Journal of Operational Research,
Vol. 122,
Issue. 3,
p.
625.
Asadi, Majid
and
Shanbhag, D.N.
2001.
Advances in Reliability.
Vol. 20,
Issue. ,
p.
199.
Khider, S.E.
Ahmed, A.-H.N.
and
Mohamed, M.K.
2002.
PRESERVATION OF SOME NEW PARTIAL ORDERINGS UNDER POISSON AND CUMULATIVE DAMAGE SHOCK MODELS.
JOURNAL OF THE JAPAN STATISTICAL SOCIETY,
Vol. 32,
Issue. 1,
p.
95.
Nanda, Asok K.
Singh, Harshinder
Misra, Neeraj
and
Paul, Prasanta
2003.
Reliability Properties of Reversed Residual Lifetime.
Communications in Statistics - Theory and Methods,
Vol. 32,
Issue. 10,
p.
2031.
Hu, Taizhong
Khaledi, Baha-Eldin
and
Shaked, Moshe
2003.
Multivariate hazard rate orders.
Journal of Multivariate Analysis,
Vol. 84,
Issue. 1,
p.
173.
Frostig, Esther
2006.
On risk dependence and mrl ordering.
Statistics & Probability Letters,
Vol. 76,
Issue. 3,
p.
231.
Ali, M. Masoom
Woo, Jungsoo
and
Nadarajah, Saralees
2008.
Stochastic Orderings of Integer Valued Random Variables.
American Journal of Mathematical and Management Sciences,
Vol. 28,
Issue. 1-2,
p.
101.
Fernández-Ponce, José María
Ortega, Eva María
and
Pellerey, Franco
2008.
CONVEX COMPARISONS FOR RANDOM SUMS IN RANDOM ENVIRONMENTS AND APPLICATIONS.
Probability in the Engineering and Informational Sciences,
Vol. 22,
Issue. 3,
p.
389.
Ortega, E.-M.
2009.
A Note on Some Functional Relationships Involving the Mean Inactivity Time Order.
IEEE Transactions on Reliability,
Vol. 58,
Issue. 1,
p.
172.
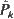 and
and  denote the probability of surviving k shocks for the first and the second device, respectively. We find conditions on the discrete distributions
denote the probability of surviving k shocks for the first and the second device, respectively. We find conditions on the discrete distributions 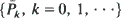 and
and 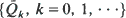 in order to obtain the failure rate order (FR), the likelihood ratio order (LR) and the mean residual order (MR) between the random lifetimes of the two devices. We also obtain sufficient conditions under which the above mentioned relations between the discrete distributions are verified in some cumulative damage shock models.
in order to obtain the failure rate order (FR), the likelihood ratio order (LR) and the mean residual order (MR) between the random lifetimes of the two devices. We also obtain sufficient conditions under which the above mentioned relations between the discrete distributions are verified in some cumulative damage shock models.