Published online by Cambridge University Press: 17 January 2023
Suppose that m drivers each choose a preferred parking space in a linear car park with n spots. In order, each driver goes to their chosen spot and parks there if possible, and otherwise takes the next available spot if it exists. If all drivers park successfully, the sequence of choices is called a parking function. Classical parking functions correspond to the case  $m=n$.
$m=n$.
We investigate various probabilistic properties of a uniform parking function. Through a combinatorial construction termed a parking function multi-shuffle, we give a formula for the law of multiple coordinates in the generic situation 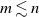 $m \lesssim n$. We further deduce all possible covariances: between two coordinates, between a coordinate and an unattempted spot, and between two unattempted spots. This asymptotic scenario in the generic situation
$m \lesssim n$. We further deduce all possible covariances: between two coordinates, between a coordinate and an unattempted spot, and between two unattempted spots. This asymptotic scenario in the generic situation 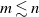 $m \lesssim n$ is in sharp contrast with that of the special situation
$m \lesssim n$ is in sharp contrast with that of the special situation  $m=n$.
$m=n$.
A generalization of parking functions called interval parking functions is also studied, in which each driver is willing to park only in a fixed interval of spots. We construct a family of bijections between interval parking functions with n cars and n spots and edge-labeled spanning trees with 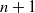 $n+1$ vertices and a specified root.
$n+1$ vertices and a specified root.