Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T19:00:34.505Z Has data issue: false hasContentIssue false
  • English
  • Français

Pareto Lévy Measures and Multivariate Regular Variation

Part of: Stochastic processes Distribution theory - Probability

Published online by Cambridge University Press:  04 January 2016

Irmingard Eder  and
Claudia Klüppelberg
Irmingard Eder*
Affiliation:
Technische Universität München
Claudia Klüppelberg*
Affiliation:
Technische Universität München
*
∗ Postal address: Centre for Mathematical Sciences, and Institute for Advanced Study, Technische Universität München, 85748 Garching, Germany.
∗ Postal address: Centre for Mathematical Sciences, and Institute for Advanced Study, Technische Universität München, 85748 Garching, Germany.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider regular variation of a Lévy process X := (Xt)t≥0 in 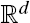with Lévy measure Π, emphasizing the dependence between jumps of its components. By transforming the one-dimensional marginal Lévy measures to those of a standard 1-stable Lévy process, we decouple the marginal Lévy measures from the dependence structure. The dependence between the jumps is modeled by a so-called Pareto Lévy measure, which is a natural standardization in the context of regular variation. We characterize multivariate regularly variation of X by its one-dimensional marginal Lévy measures and the Pareto Lévy measure. Moreover, we define upper and lower tail dependence coefficients for the Lévy measure, which also apply to the multivariate distributions of the process. Finally, we present graphical tools to visualize the dependence structure in terms of the spectral density and the tail integral for homogeneous and nonhomogeneous Pareto Lévy measures.

Keywords

Dependence of Lévy processesLévy copulaLévy measurePareto Lévy copulamultivariate regular variationmultivariate stable processspectral measuretail integraltail dependence coefficient

MSC classification

Primary: 60E07: Infinitely divisible distributions; stable distributions 60G51: Processes with independent increments; L'evy processes 60G52: Stable processes
Secondary: 60G70: Extreme value theory; extremal processes
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 44 , Issue 1 , March 2012 , pp. 117 - 138
Copyright
© Applied Probability Trust 

References

Barndorff-Nielsen, O. E. and Lindner, A. M. (2007). Lévy copulas: dynamics and transforms of Upsilon type. Scand. J. Statist. 34, 298–316.Google Scholar
Basrak, B. (2000). The sample autocorrelation function of non-linear time series. , Rijksuniversiteit Groningen.Google Scholar
Basrak, B., Davis, R. A. and Mikosch, T. (2002). A characterization of multivariate regular variation. Ann. Appl. Prob. 12, 908–920.CrossRefGoogle Scholar
Böcker, K. and Klüppelberg, C. (2010). Multivariate models for operational risk. Quant. Finance 10, 855–869.CrossRefGoogle Scholar
Bregman, Y. and Klüppelberg, C. (2005). Ruin estimation in multivariate models with Clayton dependence structure. Scand. Actuarial J.. 2005, 462–480.CrossRefGoogle Scholar
Cont, R. and Tankov, P. (2004). Financial Modelling with Jump Processes. Chapman & Hall/CRC, Boca Raton, FL.Google Scholar
De Haan, L. and Lin, T. (2001). On convergence toward an extreme value distribution in C[0,1]. Ann. Prob. 29, 467–483.Google Scholar
Eder, I. (2009). First passage events and multivariate regular variation for dependent Lévy processes with applications in insurance. , Technische Universität München.Google Scholar
Eder, I. and Klüppelberg, C. (2009). The first passage event for sums of dependent Lévy processes with applications to insurance risk. Ann. Appl. Prob. 19, 2047–2079.CrossRefGoogle Scholar
Esmaeili, H. and Klüppelberg, C. (2010). Parameter estimation of a bivariate compound Poisson process. Insurance Math. Econom. 47, 224–233.CrossRefGoogle Scholar
Esmaeili, H. and Klüppelberg, C. (2011). Parametric estimation of a bivariate stable Lévy process J. Multivariate Anal. 102, 918–930.CrossRefGoogle Scholar
Esmaeili, H. and Klüppelberg, C. (2011). Two-step estimation of a multivariate Lévy process. Submitted.Google Scholar
Giné, E., Hahn, M. G. and Vatan, P. (1990). Max-infinitely divisible and max-stable sample continuous processes. Prob. Theory Relat. Fields 87, 139–165.CrossRefGoogle Scholar
Hult, H. and Lindskog, F. (2005). Extremal behavior of regularly varying stochastic processes. Stoch. Process. Appl. 115, 249–274.CrossRefGoogle Scholar
Hult, H. and Lindskog, F. (2006). On regular variation for infinitely divisible random vectors and additive processes. Adv. Appl. Prob. 38, 134–148.CrossRefGoogle Scholar
Hult, H. and Lindskog, F. (2006). Regular variation for measures on metric spaces. Publ. Inst. Math. 80, 121–140.CrossRefGoogle Scholar
Hult, H. and Lindskog, F. (2007). Extremal behavior of stochastic integrals driven by regularly varying Lévy processes. Ann. Prob. 35, 309–339.CrossRefGoogle Scholar
Joe, H. (1997). Multivariate Models and Dependence Concepts. Chapman & Hall/CRC, London.Google Scholar
Kallenberg, O. (1983). Random Measures, 3rd edn. Akademie, Berlin.CrossRefGoogle Scholar
Kallsen, J. and Tankov, P. (2006). Characterization of dependence of multidimensional Lévy processes using Lévy copulas. J. Multivariate Anal. 97, 1551–1572.CrossRefGoogle Scholar
Klüppelberg, C. and Resnick, S. I. (2008). The Pareto copula, aggregation of risks, and the emperor's socks. J. Appl. Prob. 45, 67–84.CrossRefGoogle Scholar
Nelsen, R. (2006). An Introduction to Copulas, 2nd edn. Springer, New York.Google Scholar
Resnick, S. I. (1987). Extreme Values, Regular Variation, and Point Processes. Springer, New York.CrossRefGoogle Scholar
Resnick, S. I. (2007). Heavy-Tail Phenomena. Springer, New York.Google Scholar
Samorodnitsky, G. and Taqqu, M. S. (1994). Stable Non-Gaussian Random Processes. Chapman & Hall, New York.Google Scholar
Sato, K.-I. (1999). Lévy Processes and Infinitely Divisible Distributions. Cambridge University Press.Google Scholar
Ueltzhöfer, F. A. J. and Klüppelberg, C. (2011). An oracle inequality for penalised projection estimation of Lévy densities from high-frequency observations. J. Nonparametric Statist. 23, 967–989.CrossRefGoogle Scholar