Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cox, J. Theodore
1980.
The time constant of first-passage percolation on the square lattice.
Advances in Applied Probability,
Vol. 12,
Issue. 4,
p.
864.
Kesten, Harry
1981.
Analyticity properties and power law estimates of functions in percolation theory.
Journal of Statistical Physics,
Vol. 25,
Issue. 4,
p.
717.
Grimmett, G. R.
1981.
Critical sponge dimensions in percolation theory.
Advances in Applied Probability,
Vol. 13,
Issue. 2,
p.
314.
Cox, J. Theodore
and
Grimmett, Geoffrey
1981.
Central limit theorems for percolation models.
Journal of Statistical Physics,
Vol. 25,
Issue. 2,
p.
237.
Cox, J. Theodore
and
Kesten, Harry
1981.
On the continuity of the time constant of first-passage percolation.
Journal of Applied Probability,
Vol. 18,
Issue. 4,
p.
809.
Aizenman, M.
Chayes, J. T.
Chayes, L.
Fr�hlich, J.
and
Russo, L.
1983.
On a sharp transition from area law to perimeter law in a system of random surfaces.
Communications in Mathematical Physics,
Vol. 92,
Issue. 1,
p.
19.
Derriennic, Yves
1983.
A remark on the time constant in first-passage percolation.
Advances in Applied Probability,
Vol. 15,
Issue. 1,
p.
214.
Grimmett, Geoffrey
and
Kesten, Harry
1984.
First-passage percolation, network flows and electrical resistances.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 66,
Issue. 3,
p.
335.
Abraham, D. B.
Chayes, J. T.
and
Chayes, L.
1984.
Random surface correlation functions.
Communications in Mathematical Physics,
Vol. 96,
Issue. 4,
p.
439.
Wierman, John C.
1985.
Random Graphs '83, Based on lectures presented at the 1st Poznań Seminar on Random Graphs.
Vol. 118,
Issue. ,
p.
349.
Kesten, Harry
1986.
École d'Été de Probabilités de Saint Flour XIV - 1984.
Vol. 1180,
Issue. ,
p.
125.
Chayes, J. T.
Chayes, L.
and
Durrett, R.
1986.
Critical behavior of the two-dimensional first passage time.
Journal of Statistical Physics,
Vol. 45,
Issue. 5-6,
p.
933.
Laanait, L.
Messager, A.
and
Ruiz, J.
1989.
Discontinuity of the Wilson string tension in the 4-dimensional lattice pure gauge Potts model.
Communications in Mathematical Physics,
Vol. 126,
Issue. 1,
p.
103.
Grimmett, Geoffrey
1989.
Percolation.
p.
25.
Grimmett, Geoffrey
1989.
Percolation.
p.
82.
Koteck�, Roman
Laanait, Lahoussine
Messager, Alain
and
Ruiz, Jean
1990.
Theq-state Potts model in the standard Pirogov-Sinai theory: Surface tensions and Wilson loops.
Journal of Statistical Physics,
Vol. 58,
Issue. 1-2,
p.
199.
Kesten, Harry
and
Zhang, Yu
1993.
The tortuosity of occupied crossings of a box in critical percolation.
Journal of Statistical Physics,
Vol. 70,
Issue. 3-4,
p.
599.
Durrett, Rick
1999.
Perplexing Problems in Probability.
p.
1.
Steele, J. Michael
and
Zhang, Yu
2003.
Nondifferentiability of the time constants of first-passage percolation.
The Annals of Probability,
Vol. 31,
Issue. 2,
Wierman, John C.
2004.
Encyclopedia of Statistical Sciences.
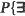 a self-avoiding path of at least n steps starting at the origin and with passage time ≦ an} ≦ 2 exp (–C1n).
a self-avoiding path of at least n steps starting at the origin and with passage time ≦ an} ≦ 2 exp (–C1n).