Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-24T13:10:30.707Z Has data issue: false hasContentIssue false
  • English
  • Français

On the number of jumps of random walks with a barrier

Part of: Distribution theory - Probability Stochastic processes Graph theory Limit theorems

Published online by Cambridge University Press:  01 July 2016

Alex Iksanov  and
Martin Möhle
Alex Iksanov*
Affiliation:
National Taras Shevchenko University
Martin Möhle*
Affiliation:
University of Düsseldorf
*
∗ Postal address: Faculty of Cybernetics, National Taras Shevchenko University, 01033 Kiev, Ukraine. Email address: [email protected]
∗∗ Postal address: Mathematical Institute, University of Düsseldorf, 40225 Düsseldorf, Germany. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let S0 := 0 and Sk := ξ1 + ··· + ξk for k ∈ ℕ := {1, 2, …}, where {ξk : k ∈ ℕ} are independent copies of a random variable ξ with values in ℕ and distribution pk := P{ξ = k}, k ∈ ℕ. We interpret the random walk {Sk : k = 0, 1, 2, …} as a particle jumping to the right through integer positions. Fix n ∈ ℕ and modify the process by requiring that the particle is bumped back to its current state each time a jump would bring the particle to a state larger than or equal to n. This constraint defines an increasing Markov chain {Rk(n) : k = 0, 1, 2, …} which never reaches the state n. We call this process a random walk with barrier n. Let Mn denote the number of jumps of the random walk with barrier n. This paper focuses on the asymptotics of Mn as n tends to ∞. A key observation is that, under p1 > 0, {Mn : n ∈ ℕ} satisfies the distributional recursion M1 = 0 and 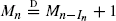for n = 2, 3, …, where In is independent of M2, …, Mn−1 with distribution P{In = k} = pk / (p1 + ··· + pn−1), k ∈ {1, …, n − 1}. Depending on the tail behavior of the distribution of ξ, several scalings for Mn and corresponding limiting distributions come into play, including stable distributions and distributions of exponential integrals of subordinators. The methods used in this paper are mainly probabilistic. The key tool is to compare (couple) the number of jumps, Mn, with the first time, Nn, when the unrestricted random walk {Sk : k = 0, 1, …} reaches a state larger than or equal to n. The results are applied to derive the asymptotics of the number of collision events (that take place until there is just a single block) for β(a, b)-coalescent processes with parameters 0 < a < 2 and b = 1.

Keywords

Absorption timebeta coalescentcouplingexponential integralMittag-Leffler distributionrandom recursive equationrandom walkstable limitsubordinator

MSC classification

Primary: 60F05: Central limit and other weak theorems 60G50: Sums of independent random variables; random walks
Secondary: 05C05: Trees 60E07: Infinitely divisible distributions; stable distributions
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 40 , Issue 1 , March 2008 , pp. 206 - 228
Copyright
Copyright © Applied Probability Trust 2008 

References

Alsmeyer, G. (1991). Some relations between harmonic renewal measures and certain first passage times. Statist. Prob. Lett. 12, 19–27.Google Scholar
Alsmeyer, G., Iksanov, A. and Rösler, U. (2007). On distributional properties of perpetuities. Submitted.Google Scholar
Bai, Z. D., Hwang, H. K. and Liang, W. Q. (1998). Normal approximations of the number of records in geometrically distributed random variables. Random Structures Algorithms 13, 319–334.3.0.CO;2-Y>CrossRefGoogle Scholar
Barbour, A. D. and Gnedin, A. V. (2006). Regenerative compositions in the case of slow variation. Stoch. Process. Appl. 116, 1012–1047.CrossRefGoogle Scholar
Basdevant, A. L. and Goldschmidt, C. (2007). Asymptotics of the allele frequency spectrum associated with the Bolthausen–Sznitman coalescent. Submitted.Google Scholar
Berestycki, J., Berestycki, N. and Schweinsberg, J. (2007). Small time behavior of beta coalescents. To appear in Ann. Inst. H. Poincaré Prob. Statist. Google Scholar
Bertoin, J. and Yor, M. (2001). On subordinators, self-similar Markov processes and some factorization of the exponential variable. Electron. Commun. Prob. 6, 95–106.CrossRefGoogle Scholar
Bingham, N. H. (1972). Limit theorems for regenerative phenomena, recurrent events and renewal theory. Z. Wahrscheinlichkeitsth. 21, 20–44.CrossRefGoogle Scholar
Bingham, N.H., Goldie, C.M. and Teugels, J. L. (1989). Regular Variation. Cambridge University Press.Google Scholar
Carmona, P., Petit, F. and Yor, M. (1997). On the distribution and asymptotic results for exponential functionals of Lévy processes. In Exponential Functionals and Principal Values Related to Brownian Motion, ed. Yor, M., Rev. Mate. Iberoamericana, Madrid, pp. 73–121.Google Scholar
Cramer, M. and Rüschendorf, L. (1995). Analysis of recursive algorithms by the contraction method. In Athens Conference on Applied Probability and Time Series Analysis, Vol. 1, Springer, New York, pp. 18–33.Google Scholar
De Haan, L. and Resnick, S. I. (1979). Conjugate Π-variation and process inversion. Ann. Prob. 7, 1028–1035.CrossRefGoogle Scholar
Delmas, J. F., Dhersin, J. S. and Siri-Jegousse, A. (2007). Asymptotic results on the length of coalescent trees. To appear in Ann Appl. Prob. Google Scholar
Drmota, M., Iksanov, A., Möhle, M. and Rösler, U. (2006). A limiting distribution for the number of cuts needed to isolate the root of a random recursive tree. To appear in Random Structures Algorithms.Google Scholar
Drmota, M., Iksanov, A., Möhle, M. and Rösler, U. (2007). Asymptotic results concerning the total branch length of the Bolthausen–Sznitman coalescent. Stoch. Process. Appl. 117, 1404–1421.CrossRefGoogle Scholar
Erickson, K. B. (1970). Strong renewal theorems with infinite mean. Trans. Amer. Math. Soc. 151, 263–291.Google Scholar
Feller, W. (1949). Fluctuation theory of recurrent events. Trans. Amer. Math. Soc. 67, 98–119.Google Scholar
Gnedin, A. V. (2004). The Bernoulli sieve. Bernoulli 10, 79–96.CrossRefGoogle Scholar
Gnedin, A. and Yakubovich, Y. (2007). On the number of collisions in Λ-coalescents. Electron. J. Prob. 12, 1547–1567.Google Scholar
Gnedin, A., Pitman, J. and Yor, M. (2006). Asymptotic laws for compositions derived from transformed subordinators. Ann. Prob. 34, 468–492.CrossRefGoogle Scholar
Gnedin, A., Pitman, J. and Yor, M. (2006). Asymptotic laws for regenerative compositions: gamma subordinators and the like. Prob. Theory Relat. Fields 135, 576–602.Google Scholar
Heyde, C. C. (1967). A limit theorem for random walks with drift. J. Appl. Prob. 4, 144–150.CrossRefGoogle Scholar
Hinderer, K. and Walk, H. (1972). Anwendungen von Erneuerungstheoremen und Taubersätzen für eine Verallgemeinerung der Erneuerungsprozesse. Math. Z. 126, 95–115.CrossRefGoogle Scholar
Iksanov, A. and Möhle, M. (2007). A probabilistic proof of a weak limit law for the number of cuts needed to isolate the root of a random recursive tree. Electron. Commun. Prob. 12, 28–35.Google Scholar
Iksanov, A. and Möhle, M. (2007). On a random recursion related to absorption times of death Markov chains. Preprint. Available at www.arxiv.org.Google Scholar
Iksanov, A., Marynych, A. and Möhle, M. (2007). On the number of collisions in beta(2,b)-coalescents. Submitted.Google Scholar
Möhle, M. (2006). On the number of segregating sites for populations with large family sizes. Adv. Appl. Prob. 38, 750–767.Google Scholar
Neininger, R. and Rüschendorf, L. (2004). On the contraction method with degenerate limit equation. Ann. Prob. 32, 2838–2856.CrossRefGoogle Scholar
Panholzer, A. (2003). Non-crossing trees revisited: cutting down and spanning subtrees. In Discrete Mathematics and Theoretical Computer Science, pp. 265–276.CrossRefGoogle Scholar
Panholzer, A. (2006). Cutting down very simple trees. Quest. Math. 29, 211–227.CrossRefGoogle Scholar
Petersen, L. C. (1982). On the relation between the multidimensional moment problem and the one-dimensional moment problem. Math. Scand. 51, 361–366.Google Scholar
Pitman, J. (1999). Coalescents with multiple collisions. Ann. Prob. 27, 1870–1902.Google Scholar
Port, S. C. (1964). Some theorems on functionals of Markov chains. Ann. Math. Statist. 35, 1275–1290.Google Scholar
Rösler, U. (1991). A limit theorem for “Quicksort”. RAIRO Inform. Théor. Appl. 25, 85–100.CrossRefGoogle Scholar
Rösler, U. and Rüschendorf, L. (2001). The contraction method for recursive algorithms. Algorithmica 29, 3–33.Google Scholar
Ross, S. M. (1982). A simple heuristic approach to simplex efficiency. Europ. J. Operat. Res. 9, 344–346.Google Scholar
Sagitov, S. (1999). The general coalescent with asynchronous mergers of ancestral lines. J. Appl. Prob. 36, 1116–1125.Google Scholar
Urbanik, K. (1992). Functionals on transient stochastic processes with independent increments. Studia Math. 103, 299–315.CrossRefGoogle Scholar
Van Cutsem, B. and Ycart, B. (1994). Renewal-type behaviour of absorption times in Markov chains. Adv. Appl. Prob. 26, 988–1005.Google Scholar
Vervaat, W. (1979). On a stochastic difference equation and a representation of nonnegative infinitely divisible random variables. Adv. Appl. Prob. 11, 750–783.CrossRefGoogle Scholar