Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kagan, Y. Y.
and
Knopoff, L.
1985.
The first-order statistical moment of the seismic moment tensor.
Geophysical Journal International,
Vol. 81,
Issue. 2,
p.
429.
Berger, M. A.
and
Roberts, P. H.
1988.
On the winding number problem with finite steps.
Advances in Applied Probability,
Vol. 20,
Issue. 2,
p.
261.
Berger, M. A.
and
Roberts, P. H.
1988.
On the winding number problem with finite steps.
Advances in Applied Probability,
Vol. 20,
Issue. 2,
p.
261.
Winch, D.E.
and
Roberts, P.H.
1995.
Derivatives of addition theorems for Legendre functions.
The Journal of the Australian Mathematical Society. Series B. Applied Mathematics,
Vol. 37,
Issue. 2,
p.
212.
1999.
Directional Statistics.
p.
395.
Wisnieff, Cynthia
Liu, Tian
Spincemaille, Pascal
Wang, Shuai
Zhou, Dong
and
Wang, Yi
2013.
Magnetic susceptibility anisotropy: Cylindrical symmetry from macroscopically ordered anisotropic molecules and accuracy of MRI measurements using few orientations.
NeuroImage,
Vol. 70,
Issue. ,
p.
363.
Soward FRS, Andrew Michael
2024.
Paul Harry Roberts. 13 September 1929—17 November 2022.
Biographical Memoirs of Fellows of the Royal Society,
Vol. 76,
Issue. ,
p.
365.
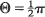 , to reduce to the Roberts-Ursell distribution for random walk on a sphere. Some diffusion limits are examined.
, to reduce to the Roberts-Ursell distribution for random walk on a sphere. Some diffusion limits are examined.