Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T18:35:31.206Z Has data issue: false hasContentIssue false
  • English
  • Français

On queueing systems with renewal departure processes

Published online by Cambridge University Press:  01 July 2016

Mark Berman  and
Mark Westcott
Mark Berman*
Affiliation:
CSIRO Division of Mathematics and Statistics, Sydney
Mark Westcott*
Affiliation:
CSIRO Division of Mathematics and Statistics, Canberra
*
∗Postal address: CSIRO Division of Mathematics and Statistics, P.O. Box 218, Lindfield, NSW 2070, Australia.
∗∗Postal address: CSIRO Division of Mathematics and Statistics, P.O. Box 1965, Canberra City, ACT 2601, Australia.
Get access Rights & Permissions [Opens in a new window]

Abstract

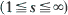It is proved that, for a large class of stable stationary queueing systems with renewal arrival processes and without losses, a necessary condition for the departure process also to be a renewal process is that its interval distribution be the same as that of the arrival process. This result is then applied to the classical GI/G/s queueing systems. In particular, alternative proofs of known characterizations of the M/G/1 and GI/M/1 systems are given, as well as a characterization of the GI/G/∞ system. In the course of the proofs, sufficient conditions for the existence of all the moments of the stationary queue-size distributions of both the GI/G/1 and GI/G/∞ systems are derived.

Keywords

RENEWAL PROCESSPOISSON PROCESSREGENERATIVE PROCESSSTATIONARITYSTABILITYGI/G/s QUEUEING SYSTEMINTERVAL DISTRIBUTIONPROBABILITY GENERATING FUNCTION
Type
Research Article
Information
Advances in Applied Probability , Volume 15 , Issue 3 , September 1983 , pp. 657 - 673
Copyright
Copyright © Applied Probability Trust 1983 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Burke, P. J. (1956) The output of a queueing system. Operat. Res. 4, 669–704.CrossRefGoogle Scholar
Cohen, J. W. (1969) The Single Server Queue. North-Holland, Amsterdam.Google Scholar
Cox, D. R. (1962) Renewal Theory. Methuen, London.Google Scholar
Daley, D. J. (1968) The correlation structure of the output process of some single server queueing systems. Ann. Math. Statist. 39, 1007–1019.CrossRefGoogle Scholar
Daley, D. J. (1971) Weakly stationary point processes and random measures. J. R. Statist. Soc. B 33, 406–428.Google Scholar
Daley, D. J. and Shanbhag, D. N. (1975) Independent inter-departure times in M/G/1/N queues. J. R. Statist. Soc. B 37, 259–263.Google Scholar
Disney, R. I., Farrell, R. L. and Demorais, P. R. (1973) A characterization of M/G/1 queues with renewal departure processes. Management Sci. 19, 1222–1228.CrossRefGoogle Scholar
Doob, J. L. (1953) Stochastic Processes. Wiley, New York.Google Scholar
Feller, W. (1971) An Introduction to Probability Theory and its Applications, Vol. 2, 2nd edn. Wiley, New York.Google Scholar
Finch, P. D. (1959) The output of the queueing system M/G/1. J. R. Statist. Soc. B 21, 375–380.Google Scholar
Karlin, S. and Taylor, H. M. (1975) A First Course in Stochastic Processes, 2nd edn. Academic Press, New York.Google Scholar
Kiefer, J. and Wolfowitz, J. (1955) On the theory of queues with many servers. Trans. Amer. Math. Soc. 78, 1–18.CrossRefGoogle Scholar
Lindley, D. V. (1952) The theory of queues with a single server. Proc. Camb. Phil. Soc. 48, 277–289.CrossRefGoogle Scholar
Puri, P. S. (1978) A limit theorem for point processes with applications. J. Appl. Prob. 15, 726–747.CrossRefGoogle Scholar
Reich, E. (1957) Waiting times when queues are in tandem. Ann. Math. Statist. 28, 768–773.CrossRefGoogle Scholar
Smith, W. L. (1955) Regenerative stochastic processes. Proc. R. Soc. London A 232, 6–31.Google Scholar
Smith, W. L. (1958) Renewal theory and its ramifications. J. R. Statist. Soc. B 20, 243–302.Google Scholar
Smith, W. L. (1959) On the cumulants of renewal processes. Biometrika 46, 1–29.CrossRefGoogle Scholar
Stidham, S. (1972) Regenerative processes in the theory of queues, with applications to the alternating-priority queue. Adv. Appl. Prob. 4, 542–577.CrossRefGoogle Scholar
Stone, C. (1968) On a theorem by Dobrushin. Ann. Math. Statist. 39, 1391–1401.CrossRefGoogle Scholar
Titchmarsh, E. C. (1939) The Theory of Functions, 2nd edn. Clarendon Press, Oxford.Google Scholar
Vere-Jones, D. (1968) Some applications of probability generating functionals to the study of input-output streams. J. R. Statist. Soc. B 30, 321–333.Google Scholar
Whitt, W. (1972) Embedded renewal processes in the GI/G/s queue. J. Appl. Prob. 9, 650–658.CrossRefGoogle Scholar