Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T01:13:09.876Z Has data issue: false hasContentIssue false
  • English
  • Français

On level crossings for a general class of piecewise-deterministic Markov processes

Part of: Markov processes Stochastic processes

Published online by Cambridge University Press:  01 July 2016

K. Borovkov  and
G. Last
K. Borovkov*
Affiliation:
University of Melbourne
G. Last*
Affiliation:
Universität Karlsruhe
*
∗ Postal address: Department of Mathematics and Statistics, The University of Melbourne, Parkville, VIC 3010, Australia. Email address: [email protected]
∗∗ Postal address: Institut für Stochastik, Universität Karlsruhe (TH), D-76128 Karlsruhe, Germany. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

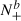We consider a piecewise-deterministic Markov process (Xt) governed by a jump intensity function, a rate function that determines the behaviour between jumps, and a stochastic kernel describing the conditional distribution of jump sizes. The paper deals with the point process of upcrossings of some level b by (Xt). We prove a version of Rice's formula relating the stationary density of (Xt) to level crossing intensities and show that, for a wide class of processes (Xt), as b → ∞, the scaled point process 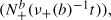where ν+(b) denotes the intensity of upcrossings of b, converges weakly to a geometrically compound Poisson process.

Keywords

Level crossingRice's formulacompound Poisson limit theorempiecewise-deterministic Markov process

MSC classification

Primary: 60J75: Jump processes 60G55: Point processes
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 40 , Issue 3 , September 2008 , pp. 815 - 834
Copyright
Copyright © Applied Probability Trust 2008 

References

Aldous, D. (1989). Probability Approximations via the Poisson Clumping Heuristic. Springer, New York.Google Scholar
Asmussen, S. (2003). Applied Probability and Queues, 2nd edn. Springer, New York.Google Scholar
Baccelli, F. and Brémaud, P. (1994). Elements of Queueing Theory. Springer, Berlin.Google Scholar
Bar-David, I. and Nemirovsky, A. (1972). Level crossings of nondifferentiable shot processes. IEEE Trans. Inf. Theory 18, 27–34.Google Scholar
Borovkov, A. A. (1976). Stochastic Processes in Queueing Theory. Springer, New York.CrossRefGoogle Scholar
Borovkov, K. A. and Novikov, A. A. (2001). On a piece-wise deterministic Markov process model. Statist. Prob. Lett. 53, 421–428.Google Scholar
Borovkov, K. and Vere-Jones, D. (2000). Explicit formulae for stationary distributions of stress release processes. J. Appl. Prob. 37, 315–321.Google Scholar
Brill, P. H. and Posner, M. J. M. (1977). Level crossings in point processes applied to queues: single server case. Operat. Res. 25, 662–673.Google Scholar
Browne, S. and Sigman, K. (1992). Work-modulated queues with applications to storage processes. J. Appl. Prob. 29, 699–712.Google Scholar
Costa, O. L. V. (1990). Stationary distributions for piecewise-deterministic Markov processes. J. Appl. Prob. 27, 60–73.Google Scholar
Davis, M. H. A. (1993). Markov Models and Optimization. Chapman and Hall, London.Google Scholar
Doshi, B. (1992). Level-crossing analysis of queues. In Queueing and Related Models, eds Basawa, I. and Bhat, U. N., Oxford University Press, pp. 3–33.Google Scholar
Falk, M., Hüsler, J. and Reiss, R.-D. (2004). Laws of Small Numbers: Extremes and Rare Events. Birkhäuser, Basel.Google Scholar
Harrison, J. M. and Resnick, S. I. (1976). The stationary distribution and first exit probabilities of a storage process with general release rule. Math. Operat. Res. 1, 347–358.Google Scholar
Kallenberg, O. (2002). Foundations of Modern Probability, 2nd edn. Springer, New York.Google Scholar
Keilson, J. and Mermin, N. D. (1959). The second-order distribution of integrand shot noise. IRE Trans. IT-5, 75–77.Google Scholar
Konstantopoulos, T. (1989). A comment on the paper ‘On the intensity of crossings by a shot noise process’. Adv. Appl. Prob. 21, 473–474.CrossRefGoogle Scholar
Kratz, M. F. (2006). Level crossings and other level functionals of stationary Gaussian processes. Prob. Surv. 3, 230–288.Google Scholar
Last, G. (2004). Ergodicity properties of stress release, repairable system and workload models. Adv. Appl. Prob. 36, 471–498.Google Scholar
Last, G. and Brandt, A. (1995). Marked Point Processes on the Real Line. Springer, New York.Google Scholar
Last, G. and Szekli, R. (1998). Stochastic comparison of repairable systems. J. Appl. Prob. 35, 348–370.Google Scholar
Leadbetter, M. R. (1966). On crossings of levels and curves by a wide class of stochastic processes. Ann. Math. Statist. 37, 260–267.Google Scholar
Leadbetter, M. R. and Hsing, T. (1990). Limit theorems for strongly mixing stationary random measures. Stoch. Process. Appl. 36, 231–243.Google Scholar
Leadbetter, M. R. and Spaniolo, G. V. (2002). On statistics at level crossings by a stationary process. Statistica Neerlandica 56, 152–164.Google Scholar
Lindgren, G., Leadbetter, M. R. and Rootzen, H. (1983). Extremes and Related Properties of Stationary Sequences and Processes. Springer, New York.Google Scholar
Meyn, S. P. and Tweedie, R. L. (1993). Stability of Markovian processes. II. Continuous-time processes and sampled chains. Adv. Appl. Prob. 25, 487–517.Google Scholar
Meyn, S. P. and Tweedie, R. L. (1993). Stability of Markovian processes. III. Foster–Lyapunov criteria for continuous-time processes. Adv. Appl. Prob. 25, 518–548.Google Scholar
Rice, S. O. (1944). Mathematical analysis of random noise. Bell System Tech. J. 24, 46–156.CrossRefGoogle Scholar
Rootzen, H. (1988). Maxima and exceedances of stationary Markov chains. Adv. Appl. Prob. 20, 371–390.Google Scholar
Vere-Jones, D. (1988). On the variance properties of stress release models. Austral. J. Statist. 30A, 123–135.Google Scholar
Zheng, X. (1991). Ergodic theorems for stress release processes. Stoch. Process. Appl. 37, 239–258.Google Scholar