Hostname: page-component-5c6d5d7d68-txr5j Total loading time: 0 Render date: 2024-09-01T11:28:43.099Z Has data issue: false hasContentIssue false
  • English
  • Français

On estimating the variance of the offspring distribution in a simple branching process

Published online by Cambridge University Press:  01 July 2016

C. C. Heyde
C. C. Heyde*
Affiliation:
Australian National University
Get access Rights & Permissions [Opens in a new window]

Abstract

A single realization {Zn, 0 ≦n≦N + 1} of a supercritical Galton-Watson process (so called) is considered and it is required to estimate the variance of the offspring distribution. A prospective estimator is proposed, where 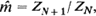, and is shown to be strongly consistent on the non-extinction set. A central limit result and an iterated logarithm result are provided to give information on the rate of convergence of the estimator. It is also shown that the estimation results are robust in the sense that they continue to apply unchanged in the case where immigration occurs. Martingale limit theory is employed at each stage in obtaining the limit results.

Keywords

BRANCHING PROCESSESGALTON-WATSON PROCESSESESTIMATIONCONSISTENCYCENTRAL LIMIT THEOREMITERATED LOGARITHM LAWMARTINGALESROBUSTNESS
Type
Research Article
Information
Advances in Applied Probability , Volume 6 , Issue 3 , September 1974 , pp. 421 - 433
Copyright
Copyright © Applied Probability Trust 1974 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
[2] Brown, B. M. (1970) Characteristic functions, moments and the central limit theorem. Ann. Math. Statist. 41, 658–664.Google Scholar
[3] Brown, B. M. (1971) Martingale central limit theorems. Ann. Math. Statist. 42, 59–66.Google Scholar
[4] Heyde, C. C. (1970) Extension of a result of Seneta for the super-critical Galton-Watson process. Ann. Math. Statist. 41, 739–742.CrossRefGoogle Scholar
[5] Heyde, C. C. and Brown, B. M. (1971) An invariance principle and some convergence rate results for branching processes. Z. Wahrscheinlichkeitsth. 20, 271–278.Google Scholar
[6] Heyde, C. C. and Leslie, J. R. (1971) Improved classical limit analogues for Galton-Watson processes with or without immigration. Bull. Austral. Math. Soc. 5, 145–155.Google Scholar
[7] Heyde, C. C. and Scott, D. J. (1973) Invariance principles for the law of the iterated logarithm for martingales and processes with stationary increments. Ann. Prob. 1, 428–436.Google Scholar
[8] Heyde, C. C. and Seneta, E. (1972) The simple branching process, a turning point test and a fundamental inequality: A historical note on I. J. Bienaymé. Biometrika, 59, 680–683.Google Scholar
[9] Loéve, M. (1963) Probability Theory. (3rd ed.) Van Nostrand, Princeton, N. J. Google Scholar
[10] Nagaev, A. V. (1967) On estimating the number of direct descendants of a particle in a branching process. Theor. Probability Appl. 12, 314–320.Google Scholar