Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Smit, J. C.
1979.
Beware of averages!.
Statistica Neerlandica,
Vol. 33,
Issue. 2,
p.
65.
Lawrance, A. J.
and
Lewis, P. A. W.
1981.
A new autoregressive time series model in exponential variables (NEAR(1)).
Advances in Applied Probability,
Vol. 13,
Issue. 4,
p.
826.
LePage, Raoul
1981.
Probability in Banach Spaces III.
Vol. 860,
Issue. ,
p.
279.
Lawrance, A. J.
and
Lewis, P. A. W.
1981.
A new autoregressive time series model in exponential variables (NEAR(1)).
Advances in Applied Probability,
Vol. 13,
Issue. 4,
p.
826.
Wolfe, Stephen James
1982.
On a continuous analogue of the stochastic difference equation Xn=ρXn-1+Bn.
Stochastic Processes and their Applications,
Vol. 12,
Issue. 3,
p.
301.
Lawrance, A. J.
and
Lewis, P. A. W.
1982.
Applied Probability-Computer Science: The Interface Volume 1.
p.
353.
Steutel, F. W.
Vervaat, W.
and
Wolfe, S. J.
1983.
Integer-valued branching processes with immigration.
Advances in Applied Probability,
Vol. 15,
Issue. 4,
p.
713.
Steutel, F. W.
Vervaat, W.
and
Wolfe, S. J.
1983.
Integer-valued branching processes with immigration.
Advances in Applied Probability,
Vol. 15,
Issue. 4,
p.
713.
Pakes, Anthony G.
1983.
SOME PROPERTIES OF A RANDOM LINEAR DIFFERENCE EQUATION1.
Australian Journal of Statistics,
Vol. 25,
Issue. 2,
p.
345.
Roerdink, J.B.T.M.
1983.
Approximate solution methods for linear stochastic difference equations.
Physica A: Statistical Mechanics and its Applications,
Vol. 119,
Issue. 3,
p.
455.
Wolfe, Stephen James
1983.
Continuity properties of decomposable probability measures on euclidean spaces.
Journal of Multivariate Analysis,
Vol. 13,
Issue. 4,
p.
534.
Runnenburg, J.Th.
1985.
PROBABILITY THEORY AND ITS APPLICATIONS.
Statistica Neerlandica,
Vol. 39,
Issue. 2,
p.
181.
Lewis, P. A. W.
1985.
SOME SIMPLE MODELS FOR CONTINUOUS VARIATE TIME SERIES1.
JAWRA Journal of the American Water Resources Association,
Vol. 21,
Issue. 4,
p.
635.
Resnick, Sidney I.
1986.
Point processes, regular variation and weak convergence.
Advances in Applied Probability,
Vol. 18,
Issue. 1,
p.
66.
Brandt, Andreas
1986.
The stochastic equation Yn
+1=AnYn + Bn
with stationary coefficients.
Advances in Applied Probability,
Vol. 18,
Issue. 01,
p.
211.
Pourahmadi, Mohsen
1986.
ON STATIONARITY OF THE SOLUTION OF A DOUBLY STOCHASTIC MODEL.
Journal of Time Series Analysis,
Vol. 7,
Issue. 2,
p.
123.
Kashara, Yuji
1986.
Stochastic Processes and Their Applications.
Vol. 1203,
Issue. ,
p.
90.
Resnick, Sidney I.
1986.
Point processes, regular variation and weak convergence.
Advances in Applied Probability,
Vol. 18,
Issue. 1,
p.
66.
Brennan, Michael D.
1986.
Length laws for random subdivision of longest intervals.
Stochastic Processes and their Applications,
Vol. 22,
Issue. 1,
p.
17.
Brandt, Andreas
1986.
The stochastic equation Yn+1=AnYn + Bn with stationary coefficients.
Advances in Applied Probability,
Vol. 18,
Issue. 1,
p.
211.
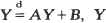 and (A, B) independent, and the convergence w.p. 1 of ∑ A1A2 ··· An-1Bn. A second subject is the series ∑ Cnf(Tn) with (Cn) a sequence of i.i.d. random variables, (Tn) the sequence of points of a Poisson process and f a Borel function on (0, ∞). The resulting random variable turns out to be infinitely divisible, and its Lévy–Hinčin representation is obtained. The two subjects coincide in case An and Cn are independent, Bn = AnCn, An = U1/αn with Un a uniform random variable, f(x) = e−x/α.
and (A, B) independent, and the convergence w.p. 1 of ∑ A1A2 ··· An-1Bn. A second subject is the series ∑ Cnf(Tn) with (Cn) a sequence of i.i.d. random variables, (Tn) the sequence of points of a Poisson process and f a Borel function on (0, ∞). The resulting random variable turns out to be infinitely divisible, and its Lévy–Hinčin representation is obtained. The two subjects coincide in case An and Cn are independent, Bn = AnCn, An = U1/αn with Un a uniform random variable, f(x) = e−x/α.