Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T20:54:04.606Z Has data issue: false hasContentIssue false
  • English
  • Français

The odds algorithm based on sequential updating and its performance

Part of: Stochastic processes

Published online by Cambridge University Press:  01 July 2016

F. Thomas Bruss  and
Guy Louchard
F. Thomas Bruss*
Affiliation:
Université Libre de Bruxelles
Guy Louchard*
Affiliation:
Université Libre de Bruxelles
*
∗ Postal address: Université Libre de Bruxelles, Département de Mathématique, Facultés des Sciences, CP 210, Boulevard du Triomphe, B-1050 Bruxelles, Belgium. Email address: [email protected]
∗∗ Postal address: Université Libre de Bruxelles, Département d'Informatique, Facultés des Sciences, CP 212, Boulevard du Triomphe, B-1050 Bruxelles, Belgium. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let I1,I2,…,In be independent indicator functions on some probability space 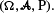We suppose that these indicators can be observed sequentially. Furthermore, let T be the set of stopping times on (Ik), k=1,…,n, adapted to the increasing filtration 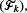where 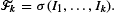The odds algorithm solves the problem of finding a stopping time τ ∈ T which maximises the probability of stopping on the last Ik=1, if any. To apply the algorithm, we only need the odds for the events {Ik=1}, that is, rk=pk/(1-pk), where 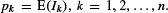The goal of this paper is to offer tractable solutions for the case where the pk are unknown and must be sequentially estimated. The motivation is that this case is important for many real-world applications of optimal stopping. We study several approaches to incorporate sequential information. Our main result is a new version of the odds algorithm based on online observation and sequential updating. Questions of speed and performance of the different approaches are studied in detail, and the conclusiveness of the comparisons allows us to propose always using this algorithm to tackle selection problems of this kind.

Keywords

Optimal stoppingsequential estimationalgorithmic performancesimulationasymptotic studiesclinical trialssecretary problem

MSC classification

Primary: 60G40: Stopping times; optimal stopping problems; gambling theory
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 41 , Issue 1 , March 2009 , pp. 131 - 153
Copyright
Copyright © Applied Probability Trust 2009 

References

Ano, K., Tamaki, M. and Hu, M. (1996). A secretary problem with uncertain employment when the number of offers is restricted. J. Operat. Res. Soc. Japan 39, 307–315.Google Scholar
Bruss, F. T. (2000). Sum the odds to one and stop. Ann. Prob. 28, 1384–1391.Google Scholar
Bruss, F. T. (2003). A note on the odds theorem of optimal stopping. Ann. Prob. 31, 1859–1861.CrossRefGoogle Scholar
Bruss, F. T. (2006). The art of a right decision: why decision makers may want to know the odds-algorithm. Newsletter Europ. Math. Soc. 62, 14–20.Google Scholar
Bruss, F. T. and Louchard, G. (2003). Optimal stopping on patterns in strings generated by independent random variables. J. Appl. Prob. 40, 49–72.CrossRefGoogle Scholar
Bruss, F. T. and Paindaveine, D. (2000). Selecting a sequence of last successes in independent trials. J. Appl. Prob. 37, 389–399.Google Scholar
Chow, Y. S., Robbins, H. and Siegmund, D. (1991). The Theory of Optimal Stopping. Corrected republication of the 1971 Dover edition. Dover, New York.Google Scholar
Ferguson, T. S. (2006). Optimal Stopping and Applications. Available at http://www.math.ucla.edu/tom/Stopping/Contents.html.Google Scholar
Ferguson, T., Hardwick, J. and Tamaki, M. (1992). Maximizing the duration of owning a relatively best object. In Strategies for Sequential Search and Selection in Real Time (Amhurst, MA, 1990; Contemp. Math 125), American Mathematical Society, Providence, RI, pp. 35–57.Google Scholar
Hsiau, S.-R. and Yang, J.-R. (2000). A natural variation of the standard secretary problem. Statistica Sinica 10, 639–646.Google Scholar
Hsiau, S.-R. and Yang, J.-R. (2002). Selecting the last success in Markov-dependent trials. J. Appl. Prob. 39, 271–281.CrossRefGoogle Scholar
Iung, B., Levrat, E. and Thomas, E. (2007). Odds-algorithm-based opportunistic maintenance task execution for preserving product conditions. CIRP Ann. 56, 13–16.Google Scholar
Kurishima, A. and Ano, K. (2003). A note on the full-information Poisson arrival selection problem. J. Appl. Prob. 40, 1147–1154.CrossRefGoogle Scholar
Mazalov, V. V. and Tamaki, M. (2006). An explicit formula for the optimal gain in the full-information problem of owning a relatively best object. J. Appl. Prob. 43, 87–101.Google Scholar
Suchwalko, A. and Szajowski, K. (2003). On Bruss' stopping problem with general gain function. Game Theory Appl. 9, 161–171.Google Scholar
Szajowski, K. (2007). A game version of the Cowan–Zabczyk–Bruss problem. Statist. Prob. Lett. 77, 1683–1689.CrossRefGoogle Scholar
Tamaki, M. (2001). Optimal stopping on trajectories and the ballot theorem. J. Appl. Prob. 38, 946–959.Google Scholar
Van Lokeren, M. (2007). DEA mémoire en statistique. Université Libre de Bruxelles. Unpublished manuscript.Google Scholar