Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T13:23:12.354Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonexplosion of a class of semilinear equations via branching particle representations

Part of: Markov processes

Published online by Cambridge University Press:  01 July 2016

Santanu Chakraborty  and
Jose Alfredo López-Mimbela
Santanu Chakraborty*
Affiliation:
University of Texas - Pan American
Jose Alfredo López-Mimbela*
Affiliation:
CIMAT
*
∗ Postal address: Department of Mathematics, University of Texas - Pan American, 1201 West University Drive, Edinburg, TX 78539-2999, USA. Email address: [email protected]
∗∗ Postal address: CIMAT, Apartado Postal 402, Guanajuato 36000, Mexico.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider a branching particle system where an individual particle gives birth to a random number of offspring at the place where it dies. The probability distribution of the number of offspring is given by pk, k = 2, 3, …. The corresponding branching process is related to the semilinear partial differential equation 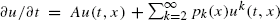for x ∈ ℝd, where A is the infinitesimal generator of a multiplicative semigroup and the pks, k = 2, 3, …, are nonnegative functions such that 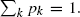We obtain sufficient conditions for the existence of global positive solutions to semilinear equations of this form. Our results extend previous work by Nagasawa and Sirao (1969) and others.

Keywords

Branching particle systemsemilinear partial differential equationglobal solution

MSC classification

Primary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Secondary: 60J85: Applications of branching processes
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 40 , Issue 1 , March 2008 , pp. 250 - 272
Copyright
Copyright © Applied Probability Trust 2008 

References

Fujita, H. (1966). On the blowing up of solutions of the Cauchy problem for ut =Δ u + u 1=α J. Fac. Sci. Univ. Tokyo 13, 109–124.Google Scholar
Ikeda, N., Nagasawa, M. and Watanabe, S. (1965). Branching Markov processes. Abstracts Proc. Japan Acad. 41, 816–821.Google Scholar
Ikeda, N., Nagasawa, M. and Watanabe, S. (1966). Branching Markov processes. Abstracts Proc. Japan Acad. 42, 252–257, 370–375, 380–384, 719–724, 1016–1021, 1022–1026.Google Scholar
Ikeda, N., Nagasawa, M. and Watanabe, S. (1968). Branching Markov processes. I. J. Math. Kyoto Univ. 8, 233–278.Google Scholar
Ikeda, N., Nagasawa, M. and Watanabe, S. (1968). Branching Markov processes. II. J. Math. Kyoto Univ. 8, 365–410.Google Scholar
López-Mimbela, J. A. (1996). A probabilistic approach to existence of global solutions of a system of nonlinear differential equations. Aportaciones Matematicas Serie Notas de Investigacion 12, 147–155.Google Scholar
López-Mimbela, J. A. and Wakolbinger, A. (1998). Length of Galton–Watson trees and blow-up of semilinear systems. J. Appl. Prob. 35, 802–811.CrossRefGoogle Scholar
Nagasawa, M. and Sirao, T. (1969). Probabilistic treatment of the blowing up of solutions for a nonlinear integral equation. Trans Amer. Math. Soc. 139, 301–310.CrossRefGoogle Scholar