Let X, Y be two sets of positive reach in ℝd. The translative integral formula says that, for 0 ≦ k ≦ d − 1 and bounded Borel subsets A, B ε ℝd, 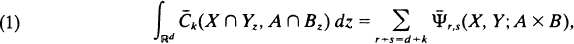where is the curvature measure (of order k) of X and 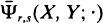is the mixed curvature measure of the sets X, Y and order r, S [1]. The mixed curvature measures are introduced by means of rectifiable currents, which leads to a relatively simple proof of (1). The proof needs an additional assumption on X, Y assuring that also reach (X ∩ Yz) > 0 for almost all z. This assumption is satisfied automatically for convex bodies, in dimension 2, or for sets with a sufficiently smooth boundary. Using the additivity of mixed curvature measures, (1) can be extended to unions of sets of positive reach.