Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-25T05:22:28.792Z Has data issue: false hasContentIssue false
  • English
  • Français

The Minimum Vertex Degree of a Graph on Uniform Points in [0, 1]d

Part of: Graph theory Combinatorial probability

Published online by Cambridge University Press:  01 July 2016

Martin J. B. Appel  and
Ralph P. Russo
Martin J. B. Appel*
Affiliation:
United Technologies Research Center
Ralph P. Russo*
Affiliation:
University of Iowa
*
∗ Postal address: United Technologies Research Center, East Hartford, CT 06108, USA.
∗∗ Postal address: Department of Statistics and Actuarial Science, University of Iowa, Iowa City, IA 52242, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

This article continues an investigation begun in [2]. A random graph Gn(x) is constructed on independent random points U1, · ··, Un distributed uniformly on [0, 1]d, d ≧ 1, in which two distinct such points are joined by an edge if the l∞-distance between them is at most some prescribed value 0 < x < 1.

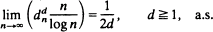Almost-sure asymptotic results are obtained for the convergence/divergence of the minimum vertex degree of the random graph, as the number n of points becomes large and the edge distance x is allowed to vary with n. The largest nearest neighbor link dn, the smallest x such that Gn(x) has no vertices of degree zero, is shown to satisfy Series and sequence criteria on edge distances {xn} are provided which guarantee the random graph to be complete, a.s. These criteria imply a.s. limiting behavior of the diameter of the vertex set.

Keywords

RANDOM GRAPHMINIMUM VERTEX DEGREELARGEST NEAREST-NEIGHBOR LINK

MSC classification

Primary: 05C80: Random graphs
Secondary: 60C05: Combinatorial probability
Type
Stochastic Geometry and Statistical Applications
Information
Advances in Applied Probability , Volume 29 , Issue 3 , September 1997 , pp. 582 - 594
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Appel, M. J. B. and Russo, R. P. (1997) Connectivity of a graph on uniform points in [0, 1] d. In preparation.Google Scholar
[2] Appel, M. J. B. and Russo, R. P. (1997) The maximum vertex degree of a graph on uniform points in [0, 1]d. Adv. Appl. Prob. 29, 567–581.Google Scholar
[3] Bollobás, B. (1979) Graph Theory: an Introductory Course. Springer, Berlin.Google Scholar
[4] Dette, H. and Henze, N. (1989) The limit distribution of the largest nearest-neighbor link in the unit d-cube. J. Appl. Prob. 26, 67–80.Google Scholar
[5] Dudley, R. M. (1978) Central limit theorems for empirical measures. Ann. Prob. 6, 899–929.CrossRefGoogle Scholar
[6] Palmer, E. M. (1985) Graphical Evolution. Wiley, New York.Google Scholar
[7] Steele, J. M. and Tierney, L. (1986) Boundary domination and the distribution of the largest nearest-neighbor link. J. Appl. Prob. 23, 524–528.Google Scholar