Article contents
Mean square rate of convergence for random walk approximation of forward-backward SDEs
Published online by Cambridge University Press: 24 September 2020
Abstract
Let (Y, Z) denote the solution to a forward-backward stochastic differential equation (FBSDE). If one constructs a random walk 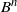 $B^n$ from the underlying Brownian motion B by Skorokhod embedding, one can show
$B^n$ from the underlying Brownian motion B by Skorokhod embedding, one can show 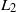 $L_2$-convergence of the corresponding solutions
$L_2$-convergence of the corresponding solutions 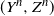 $(Y^n,Z^n)$ to
$(Y^n,Z^n)$ to 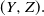 $(Y, Z).$ We estimate the rate of convergence based on smoothness properties, especially for a terminal condition function in
$(Y, Z).$ We estimate the rate of convergence based on smoothness properties, especially for a terminal condition function in 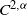 $C^{2,\alpha}$. The proof relies on an approximative representation of
$C^{2,\alpha}$. The proof relies on an approximative representation of 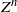 $Z^n$ and uses the concept of discretized Malliavin calculus. Moreover, we use growth and smoothness properties of the partial differential equation associated to the FBSDE, as well as of the finite difference equations associated to the approximating stochastic equations. We derive these properties by probabilistic methods.
$Z^n$ and uses the concept of discretized Malliavin calculus. Moreover, we use growth and smoothness properties of the partial differential equation associated to the FBSDE, as well as of the finite difference equations associated to the approximating stochastic equations. We derive these properties by probabilistic methods.
Keywords
- Type
- Original Article
- Information
- Copyright
- © Applied Probability Trust 2020
References
- 3
- Cited by



