Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-25T09:15:14.720Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit theorems for continuous-state branching processes with immigration

Part of: Limit theorems Markov processes

Published online by Cambridge University Press:  06 June 2022

Clément Foucart ,
Chunhua Ma  and
Linglong Yuan
Clément Foucart*
Affiliation:
Université SorbonneParis Nord
Chunhua Ma*
Affiliation:
Nankai University
Linglong Yuan*
Affiliation:
University of Liverpool, Xi’an Jiaotong-Liverpool University
*
*Postal address: Laboratoire Analyse, Géométrie & Applications, UMR 7539, Institut Galilée, Université Sorbonne Paris Nord, Villetaneuse, 93430, France. Email address: [email protected]
**Postal address: School of Mathematical Sciences and LPMC, Nankai University, Tianjin, 300071, P. R. China. Email address: [email protected]
***Postal address: Department of Mathematical Sciences, University of Liverpool, Liverpool, L69 7ZL, UK. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

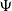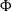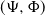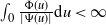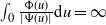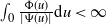A continuous-state branching process with immigration having branching mechanism $\Psi$ and immigration mechanism $\Phi$ , a CBI $(\Psi,\Phi)$ process for short, may have either of two different asymptotic regimes, depending on whether $\int_{0}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u<\infty$ or $\int_{0}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u=\infty$ . When $\int_{0}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u<\infty$ , the CBI process has either a limit distribution or a growth rate dictated by the branching dynamics. When 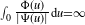$\scriptstyle\int_{0}\tfrac{\Phi(u)}{|\Psi(u)|}\textrm{d} u=\infty$ , immigration overwhelms branching dynamics. Asymptotics in the latter case are studied via a nonlinear time-dependent renormalization in law. Three regimes of weak convergence are exhibited. Processes with critical branching mechanisms subject to a regular variation assumption are studied. This article proves and extends results stated by M. Pinsky in ‘Limit theorems for continuous state branching processes with immigration’ (Bull. Amer. Math. Soc.78, 1972).

Keywords

Continuous-state branching processesimmigrationGrey’s martingalelimit distributionnonlinear renormalizationregularly varying functions

MSC classification

Primary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Secondary: 60F05: Central limit and other weak theorems 60F15: Strong theorems
Type
Original Article
Information
Advances in Applied Probability , Volume 54 , Issue 2 , June 2022 , pp. 599 - 624
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barbour, A. D. and Pakes, A. G. (1979). Limit theorems for the simple branching process allowing immigration. II. The case of infinite offspring mean. Adv. Appl. Prob. 11, 63–72.CrossRefGoogle Scholar
Barczy, M., Ben Alaya, M., Kebaier, A. and Pap, G. (2018). Asymptotic properties of maximum likelihood estimator for the growth rate for a jump-type CIR process based on continuous time observations. Stoch. Process. Appl. 128, 1135–1164.CrossRefGoogle Scholar
Bertoin, J. (1996). Lévy Processes. Cambridge University Press.Google Scholar
Bingham, N. H., Goldie, C. M. and Teugels, J. L. (1987). Regular Variation. Cambridge University Press.CrossRefGoogle Scholar
Bingham, N. H. (1976). Continuous branching processes and spectral positivity. Stoch. Process. Appl. 4, 217–242.CrossRefGoogle Scholar
Blackwell, D. and Dubins, L. E. (1983). An extension of Skorohod’s almost sure representation theorem. Proc. Amer. Math. Soc. 89, 691–692.Google Scholar
Chazal, M., Loeffen, R. and Patie, P. (2018). Smoothness of continuous state branching with immigration semigroups. J. Math. Anal. Appl. 459, 619–660.CrossRefGoogle Scholar
Cohn, H. (1977). On the convergence of the supercritical branching processes with immigration. J. Appl. Prob. 14, 387–390.CrossRefGoogle Scholar
Dawson, D. A. and Li, Z. (2012). Stochastic equations, flows and measure-valued processes. Ann. Prob. 40, 813–857.CrossRefGoogle Scholar
Duhalde, X., Foucart, C. and Ma, C. (2014). On the hitting times of continuous-state branching processes with immigration. Stoch. Process. Appl. 124, 4182–4201.CrossRefGoogle Scholar
Duffie, D., Filipović, D. and Schachermayer, M. (2003). Affine processes and applications in finance. Ann. Appl. Prob. 13, 984–1053.CrossRefGoogle Scholar
Duquesne, T. and Labbé, C. (2014). On the Eve property for CSBP. Electron. J. Prob. 19, 31 pp.CrossRefGoogle Scholar
Durrett, R. (2010). Probability: Theory and Examples, 4th edn. Cambridge University Press.CrossRefGoogle Scholar
Fittipaldi, M. C. and Fontbona, J. (2012). On SDE associated with continuous-state branching processes conditioned to never be extinct. Electron. Commun. Prob. 17, 13 pp.CrossRefGoogle Scholar
Foucart, C. and Ma, C. (2019). Continuous-state branching processes, extremal processes and super-individuals. Ann. Inst. H. Poincaré Prob. Statist. 55, 1061–1086.CrossRefGoogle Scholar
Foucart, C. and Uribe Bravo, G. (2014). Local extinction in continuous-state branching processes with immigration. Bernoulli 20, 1819–1844.CrossRefGoogle Scholar
Grey, D. R. (1974). Asymptotic behaviour of continuous time, continuous state-space branching processes. J. Appl. Prob. 11, 669–677.CrossRefGoogle Scholar
Grey, D. R. (1977). Almost-sure convergence in Markov branching process with infinite mean. J. Appl. Prob. 14, 702–716.CrossRefGoogle Scholar
Heathcote, C. R. (1965). A branching process allowing immigration. J. R. Statist. Soc. B 27, 138–143.Google Scholar
Heyde, C. C. (1970). Extension of a result of Seneta for the super-critical Galton–Watson process. Ann. Math. Statist. 41, 739–742.CrossRefGoogle Scholar
Jiao, Y., Ma, C. and Scotti, C. (2017). Alpha-CIR model with branching processes in sovereign interest rate modeling. Finance Stoch. 21, 789–813.CrossRefGoogle Scholar
Jiao, Y. (ed.) (2020). From Probability to Finance: Lecture Notes of BICMR Summer School on Financial Mathematics. Springer, Singapore.CrossRefGoogle Scholar
Kawazu, K. and Watanabe, S. (1971). Branching processes with immigration and related limit theorems. Teor. Veroyat. Primen. 16, 34–51.Google Scholar
Keller-Ressel, M. and Mijatović, A. (2012). On the limit distributions of continuous-state branching processes with immigration. Stoch. Process. Appl. 122, 2329–2345.CrossRefGoogle Scholar
Kyprianou, A. E. and Pardo, J. C. (2008). Continuous-state branching processes and self-similarity. J. Appl. Prob. 45, 1140–1160.CrossRefGoogle Scholar
Kyprianou, A. E. (2014). Fluctuations of Lévy Processes with Applications, 2nd edn. Springer, Heidelberg.CrossRefGoogle Scholar
Lambert, A. (2007). Quasi-stationary distributions and the continuous-state branching process conditioned to be never extinct. Electron. J. Prob. 12, 420–446.CrossRefGoogle Scholar
Li, Z. (2000). Asymptotic behaviour of continuous time and state branching processes. J. Austral. Math. Soc. 68, 68–84.CrossRefGoogle Scholar
Li, Z. (2011). Measure-Valued Branching Markov Processes. Springer, Berlin, Heidelberg.CrossRefGoogle Scholar
Li, Z. and Ma, C. (2008). Catalytic discrete state branching models and related limit theorems. J. Theoret. Prob. 21, 936–965.CrossRefGoogle Scholar
Pakes, A. G. (1979). Limit theorems for the simple branching process allowing immigration. I. The case of finite offspring mean. Adv. Appl. Prob. 11, 31–62.CrossRefGoogle Scholar
Pinsky, M. A. (1972) Limit theorems for continuous state branching processes with immigration. Bull. Amer. Math. Soc. 78, 242–244.CrossRefGoogle Scholar
Resnick, S. I. (2008). Extreme Values, Regular Variation and Point Processes. Springer, New York.Google Scholar
Seneta, E. (1970). On the supercritical Galton–Watson process with immigration. Math. Biosci. 7, 9–14.CrossRefGoogle Scholar