Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T19:43:19.540Z Has data issue: false hasContentIssue false
  • English
  • Français

A limit theorem for certain disordered random systems

Part of: Special processes

Published online by Cambridge University Press:  01 July 2016

Xinhong Ding
Xinhong Ding*
Affiliation:
Carleton University
*
* Postal address: Department of Mathematics and Statistics, Carleton University, Ottawa, Ontario K1S 5B6, Canada.
Get access Rights & Permissions [Opens in a new window]

Abstract

Many disordered random systems in applications can be described by N randomly coupled Ito stochastic differential equations in :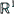

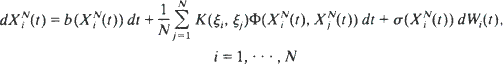
where 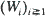is a sequence of independent copies of the one-dimensional Brownian motion W and ( 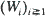is a sequence of independent copies of the ℝp-valued random vector ξ. We show that under suitable conditions on the functions b, σ, K and Φ the dynamical behaviour of this system in the N → (limit can be described by the non-linear stochastic differential equation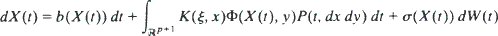

where P(t, dx dy) is the joint probability law of ξ and X(t).

Keywords

INTERACTING DIFFUSIONSMCKEAN-VLASOV LIMITNEURAL NETWORKS: SPIN GLASSES

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Type
Research Article
Information
Advances in Applied Probability , Volume 26 , Issue 4 , December 1994 , pp. 1022 - 1043
Copyright
Copyright © Applied Probability Trust 1994 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by Professor Donald A. Dawson's research grant.

References

Aldous, D. (1978) Stopping times and tightness. Ann. Prob. 6, 335–340.Google Scholar
Amit, D. J., Gutfreund, H. and Somplinsky, H. (1985) Spin-glass models of neural networks. Phys. Rev. A 32, 1007–1018.CrossRefGoogle ScholarPubMed
Bonilla, L. L. (1987) Stable nonequilibrium probability densities and phase transitions for mean-field models in the thermodynamic limit. J. Statist. Phys. 46, 659–678.Google Scholar
Bonilla, L. L. and Casado, J. M. (1989). Dynamics of a soft-spin van Hemmen model I, phase and bifurcation diagrams for stationary distributions. J. Statist. Phys. 56, 113–125.Google Scholar
Dawson, D. A. (1983) Critical dynamics and fluctuations for a mean-field model of cooperative behaviour. J. Statist. Phys. 31, 29–85.Google Scholar
Dawson, D. A. and Gärtner, J. (1989) Large deviation, free energy functional, and quasipotential for a mean field model of interacting diffusions. Mem. Amer. Math. Soc. 78, No. 398.Google Scholar
Desai, R. C. and Zwanzig, R. (1978) Statistical mechanics of a nonlinear stochastic model. J. Statist. Phys. 19, 1–24.CrossRefGoogle Scholar
Ellis, R. S. (1985) Entropy, Large Deviation, and Statistical Mechanics, Springer-Verlag, Berlin.Google Scholar
Ethier, S. N. and Kurtz, T. G. (1986) Markov Process: Characterization and Convergence. Wiley, New York.CrossRefGoogle Scholar
Gärtner, J. (1986) On the McKean-Vlasov limit for interacting diffusions I, II. Akademie der Wissenschaften der DDR Karl-Weierstrass Institut fur Mathematik, Preprint.Google Scholar
Joffe, A. and Metivier, M. (1986) Weak convergence of sequences of semimartingales with applications to multitype branching processes. Adv. Appl. Prob. 18, 20–65.Google Scholar
Léonard, C. (1984) Une loi des grands nombres pour des systèmes de diffusions avec interaction à coefficients nonbomés. Ann. Inst. H. Poincaré 22, 237–262.Google Scholar
Mckean, H. P. (1969) Propagation of chaos for a class of nonlinear parabolic equations. Lecture Series in Differential Equations 7, Catholic University, pp. 41–57. Van Nostrand Reinhold, New York.Google Scholar
Oeschläger, K. (1984) A martingale approach to the law of large numbers for weakly interacting stochastic processes. Ann. Prob. 12, 458–479.Google Scholar
Tamura, Y. (1984) On asymptotic behaviours of the solution of a non-linear diffusion equation. J. Fac. Sci. Univ. Tokyo. Sect. 1A, Math. 31, 195–221.Google Scholar
Vaillancourt, J. (1987) Interactive Fleming-Viot processes and related measure-valued processes. Thesis. Dept. of Math. and Stat., Carleton University.Google Scholar
Van Hemmen, J. L., Grensing, D., Huber, A. and Kuhn, R. (1989) Nonlinear neural networks I, II. J. Statist. Phys. 50, 231–293.Google Scholar