Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T14:00:32.685Z Has data issue: false hasContentIssue false
  • English
  • Français

Infection Spread in Random Geometric Graphs

Part of: Distribution theory Combinatorial probability Special processes Markov processes

Published online by Cambridge University Press:  04 January 2016

Ghurumuruhan Ganesan
Ghurumuruhan Ganesan*
Affiliation:
École Polytechnique Fédérale de Lausanne
*
∗ Postal address: MA B1 527, École Polytechnique Fédérale de Lausanne, Station 8, CH-1015 Lausanne, Switzerland. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study the speed of infection spread and the survival of the contact process in the random geometric graph G = G(n, rn, f) of n nodes independently distributed in S = [-½, ½]2 according to a certain density f(·). In the first part of the paper we assume that infection spreads from one node to another at unit rate and that infected nodes stay in the same state forever. We provide an explicit lower bound on the speed of infection spread and prove that infection spreads in G with speed at least D1nrn2. In the second part of the paper we consider the contact process ξt on G where infection spreads at rate λ > 0 from one node to another and each node independently recovers at unit rate. We prove that, for every λ > 0, with high probability, the contact process on G survives for an exponentially long time; there exist positive constants c1 and c2 such that, with probability at least 1 - c1 / n4, the contact process 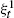starting with all nodes infected survives up to time tn = exp(c2n/logn) for all n.

Keywords

Random geometric graphspeed of infection spreadsurvival time of contact process

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces) 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 60C05: Combinatorial probability 62E10: Characterization and structure theory
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 47 , Issue 1 , March 2015 , pp. 164 - 181
Copyright
© Applied Probability Trust 

References

Chatterjee, S. and Durrett, R. (2009). Contact processes on random graphs with power-law degree distributions have critical value 0. Ann. Prob. 37, 2332–2356.Google Scholar
Durrett, R. (1984). Oriented percolation in two dimensions. Ann. Prob. 12, 999–1040.Google Scholar
Franceschetti, M., Dousse, O., Tse, D. N. C. and Thiran, P. (2007). Closing the gap in the capacity of wireless networks via percolation theory. IEEE Trans. Inf. Theory 53, 1009–1018.Google Scholar
Ganesan, G. (2013). Size of the giant component in a random geometric graph. Ann. Inst. H. Poincaré Prob. Statist. 49, 1130–1140.CrossRefGoogle Scholar
Gupta, P. and Kumar, P. R. (1999). Critical power for asymptotic connectivity in wireless networks. In Stochastic Analysis, Control, Optimization and Applications, Birkhäuser, Boston, MA, pp. 547–566.Google Scholar
Liggett, T. M. (1999). Stochastic Interacting Systems: Contact, Voter and Exclusion Processes. Springer, Berlin.Google Scholar
Meester, R. and Roy, R. (1996). Continuum Percolation. (Camb. Tracts Math. 119). Cambridge University Press.CrossRefGoogle Scholar
Mountford, T., Mourrat, J.-C., Valesin, D. and Yao, Q. (2012). Exponential extinction time of the contact process on finite graphs. Preprint. Available at http://uk.arxiv.org/abs/1203.2972.Google Scholar
Penrose, M. (2003). Random Geometric Graphs. Oxford University Press.Google Scholar
Sarkar, A. (1996). Some problems in continuum percolation. , Indian Statistical Institute, Delhi.Google Scholar
Ganesan, G. (2014). Phase transitions for Erdős–Rényi graphs. Preprint. Available at http://arxiv.org/abs/1409.2606.Google Scholar
Ganesan, G. (2014). First passage percolation with nonidentical passage times. Preprint. Available at http://arxiv.org/abs/1409.2602.Google Scholar
Smythe, R. T. and Wierman, J. C. (1978). First-Passage Percolation on the Square Lattice. Springer, Berlin.Google Scholar