Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-23T12:45:09.852Z Has data issue: false hasContentIssue false
  • English
  • Français

Implicit Renewal Theory and Power Tails on Trees

Part of: Markov processes Special processes Limit theorems Stochastic analysis

Published online by Cambridge University Press:  04 January 2016

Predrag R. Jelenković  and
Mariana Olvera-Cravioto
Predrag R. Jelenković*
Affiliation:
Columbia University
Mariana Olvera-Cravioto*
Affiliation:
Columbia University
*
∗ Postal address: Department of Electrical Engineering, Columbia University, New York, NY 10027, USA.
∗∗ Postal address: Department of Industrial Engineering and Operations Research, Columbia University, New York, NY 10027, USA. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

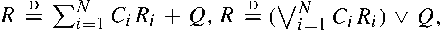We extend Goldie's (1991) implicit renewal theorem to enable the analysis of recursions on weighted branching trees. We illustrate the developed method by deriving the power-tail asymptotics of the distributions of the solutions R to and similar recursions, where (Q, N, C1, C2,…) is a nonnegative random vector with N ∈ {0, 1, 2, 3,…} ∪ {∞}, and 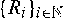are independent and identically distributed copies of R, independent of (Q, N, C1, C2,…); here ‘∨’ denotes the maximum operator.

Keywords

Implicit renewal theoryweighted branching processmultiplicative cascadestochastic recursionpower lawlarge deviationsstochastic fixed-point equation

MSC classification

Primary: 60H25: Random operators and equations
Secondary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.) 60F10: Large deviations 60K05: Renewal theory
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 44 , Issue 2 , June 2012 , pp. 528 - 561
Copyright
© Applied Probability Trust 

Footnotes

Supported by the NSF, grant no. CMMI-1131053.

Supported by the NSF, grant no. CMMI-1131053.

References

Aldous, D. J. and Bandyopadhyay, A. (2005). A survey of max-type recursive distributional equation. Ann. Appl. Prob. 15, 1047–1110.Google Scholar
Alsmeyer, G. and Kuhlbusch, D. (2010). Double martingale structure and existence of ϕ-moments for weighted branching processes. Münster J. Math. 3, 163–212.Google Scholar
Alsmeyer, G. and Meiners, M. (2012). Fixed points of inhomogeneous smoothing transforms. To appear in J. Diff. Equat. Appl. Google Scholar
Alsmeyer, G. and Rösler, U. (2005). A stochastic fixed point equation related to weighted branching with deterministic weights. Electron. J. Prob. 11, 27–56.Google Scholar
Alsmeyer, G. and Rösler, U. (2008). A stochastic fixed point equation for weighted minima and maxima. Ann. Inst. H. Poincaré Prob. Statist. 44, 89–103.Google Scholar
Alsmeyer, G., Biggins, J. D. and Meiners, M. (2012). The functional equation of the smoothing transform. To appear in Ann. Prob. Google Scholar
Athreya, K. B., McDonald, D. and Ney, P. (1978). Limit theorems for semi-Markov processes and renewal theory for Markov chains. Ann. Prob. 6, 788–797.Google Scholar
Biggins, J. D. (1977). Martingale convergence in the branching random walk. J. Appl. Prob. 14, 25–37.Google Scholar
Biggins, J. D. and Kyprianou, A. E. (1997). Seneta–Heyde norming in the branching random walk. Ann. Prob. 25, 337–360.Google Scholar
Billingsley, P. (1995). Probability and Measure, 3rd edn. Wiley-Interscience, New York.Google Scholar
Brandt, A. (1986). The stochastic equation Y n+1 = A n Y n + B n with stationary coefficients. Adv. Appl. Prob. 18, 211–220.Google Scholar
Durret, R. and Liggett, T. M. (1983). Fixed points of the smoothing transformation. Z. Wahrscheinlichkeitsth. 64, 275–301.Google Scholar
Fill, J. A. and Janson, S. (2001). Approximating the limiting Quicksort distribution. Random Structures Algorithms 19, 376–406.Google Scholar
Goldie, C. M. (1991). Implicit renewal theory and tails of solutions of random equations. Ann. Appl. Prob. 1, 126–166.CrossRefGoogle Scholar
Grincevičius, A. K. (1975). One limit distribution for a random walk on the line. Lithuanian Math. J. 15, 580–589.CrossRefGoogle Scholar
Holley, R. and Liggett, T. M. (1981). Generalized potlatch and smoothing processes. Z. Wahrscheinlichkeitsth. 55, 165–195.Google Scholar
Iksanov, A. M. (2004). Elementary fixed points of the BRW smoothing transforms with infinite number of summands. Stoch. Process. Appl. 114, 27–50.Google Scholar
Jagers, P. and Rösler, U. (2004). Stochastic fixed points for the maximum. In Mathematics and Computer Science III, eds Drmota, M. et al., Birkhäuser, Basel, pp. 325–338.CrossRefGoogle Scholar
Jelenković, P. R. and Olvera-Cravioto, M. (2010). Information ranking and power laws on trees. Adv. Appl. Prob. 42, 1057–1093.CrossRefGoogle Scholar
Kahane, J.-P. and Peyrière, J. (1976). Sur certaines martingales de Benoit Mandelbrot. Adv. Math. 22, 131–145.CrossRefGoogle Scholar
Kesten, H. (1973). Random difference equations and renewal theory for product of random matrices. Acta Math. 131, 207–248.Google Scholar
Liu, Q. (1998). Fixed points of a generalized smoothing transformation and applications to the branching random walk. Adv. Appl. Prob. 30, 85–112.CrossRefGoogle Scholar
Liu, Q. (2000). On generalized multiplicative cascades. Stoch. Process. Appl. 86, 263–286.Google Scholar
Neininger, R. and Rüschendorf, L. (2004). A general limit theorem for recursive algorithms and combinatorial structures. Ann. Appl. Prob. 14, 378–418.CrossRefGoogle Scholar
Rösler, U. (1993). The weighted branching process. In Dynamics of Complex and Irregular Systems (Bielefeld, 1991; Bielefeld Encount. Math. Phys. VIII), World Scientific, River Edge, NJ, pp. 154–165.Google Scholar
Rösler, U. and Rüschendorf, L. (2001). The contraction method for recursive algorithms. Algorithmica 29, 3–33.Google Scholar
Volkovich, Y. and Litvak, N. (2010). Asymptotic analysis for personalized web search. Adv. Appl. Prob. 42, 577–604.Google Scholar
Waymire, E. C. and Williams, S. C. (1995). Multiplicative cascades: dimension spectra and dependence. J. Fourier Anal. Appl. 1995, 589–609.Google Scholar