Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T19:51:17.822Z Has data issue: false hasContentIssue false
  • English
  • Français

Homecomings of Markov processes

Published online by Cambridge University Press:  01 July 2016

J. F. C. Kingman
J. F. C. Kingman*
Affiliation:
University of Oxford
Get access Rights & Permissions [Opens in a new window]

Abstract

If x0 is a particular state for a continuous-time Markov process X, the random time set is often of both practical and theoretical interest. Ignoring trivial or pathological cases, there are four different types of structure which this random set can display. To some extent, it is possible to treat all four cases in a unified way, but they raise different questions and require different modes of description. The distributions of various random quantities associated with 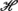can be related to one another by simple and useful formulae.

Keywords

MARKOV PROCESSREGENERATIONZERO SETLOCAL TIMESUBORDINATOR
Type
Research Article
Information
Advances in Applied Probability , Volume 5 , Issue 1 , April 1973 , pp. 66 - 102
Copyright
Copyright © Applied Probability Trust 1973 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Bartlett, M. S. (1953) Recurrence and first passage times. Proc. Camb. Phil. Soc. 49, 263–275.Google Scholar
[2] Bartlett, M. S. (1956) An Introduction to Stochastic Processes. Cambridge.Google Scholar
[3] Blackwell, D. (1948) A renewal theorem. Duke Math. J. 15, 145–150.Google Scholar
[4] Blumenthal, R. M. and Getoor, R. K. (1964) Local times for Markov processes. Z. Wahrscheinlichkeitsth. 3, 50–74.CrossRefGoogle Scholar
[5] Blumenthal, R. M. and Getoor, R. K. (1968) Markov Processes and Potential Theory. Academic Press, New York.Google Scholar
[6] Bretagnolle, J. and Dacunna-Castelle, D. (1967) Pointwise recurrence of processes with independent increments. Ann. Inst. H. Poincaré B3, 677–682.Google Scholar
[7] Chung, K. L. (1963) On the boundary theory for Markov chains. Acta Math. 110, 19–77.Google Scholar
[8] Chung, K. L. (1967) Markov Chains with Stationary Transition Probabilities. Springer, Berlin.Google Scholar
[9] Cox, D. R. (1962) Renewal Theory. Methuen, London.Google Scholar
[10] Doob, J. L. (1953) Stochastic Processes. Wiley, New York.Google Scholar
[11] Erdös, P., Feller, W. and Pollard, H. (1949) A theorem on power series. Bull. Amer. Math. Soc. 55, 201–204.CrossRefGoogle Scholar
[12] Feller, W. (1949) Fluctuation theory of recurrent events. Trans. Amer. Math. Soc. 67, 98–119.Google Scholar
[13] Feller, W. (1950) An Introduction to Probability Theory and its Applications. Wiley, New York.Google Scholar
[14] Feller, W. (1966) An Introduction to Probability Theory and its Applications, Volume II. Wiley, New York.Google Scholar
[15] Freedman, D. (1971) Brownian Motion and Diffusion. Holden-Day, San Francisco.Google Scholar
[16] Fristedt, B. E. (1973) Sample functions of stochastic processes with stationary, independent increments. Advances in Probability 3. Marcel Dekker, New York.Google Scholar
[17] Gani, J. and Prabhu, N. U. (1963) A storage model with continuous infinitely divisible inputs. Proc. Camb. Phil. Soc. 59, 417–429.Google Scholar
[18] Hoffman-J⊘rgensen, J. (1969) Markov sets. Math. Scand. 24, 145–166.Google Scholar
[19] Ito, K. and Mckean, H. P. (1965) Diffusion Processes and their Sample Paths. Springer, Berlin.Google Scholar
[20] Kendall, D. G. (1973) Foundations of a theory of random sets. Stochastic Geometry and Stochastic Analysis. Wiley, London.Google Scholar
[21] Kingman, J. F. C. (1963) On continuous time models in the theory of dams. J. Aust. Math. Soc. 3, 480–487.Google Scholar
[22] Kingman, J. F. C. (1964) On doubly stochastic Poisson processes. Proc. Camb. Phil. Soc. 60, 923–930.CrossRefGoogle Scholar
[23] Kingman, J. F. C. (1972) Regenerative Phenomena. Wiley, London.Google Scholar
[24] Kingman, J. F. C. (1973) An intrinsic description of local time. J. Lond. Math. Soc. To appear.Google Scholar
[25] Krylov, N. V. and Yuskevitch, A. A. (1964) Markov random sets. Teor. Veroyat. Primen 9, 738–743.Google Scholar
[26] Lévy, P. (1948) Processus Stochastiques et Mouvement Brownien. Paris.Google Scholar
[27] Lévy, P. (1951) Systèmes markoviens et stationnaires. Cas dénombrable. Ann. Sci. École Norm. Sup. (3) 68, 327–381.Google Scholar
[28] Lévy, P. (1952) Complément a l'étude des processus de Markoff. Ann. Sci. École Norm. Sup. (3) 69, 203–212.Google Scholar
[29] Moran, P. A. P. (1959) The Theory of Storage. Methuen, London.Google Scholar
[30] Neveu, J. (1961) Une généralisation des processus à accroissements positifs indépendents. Abh. Math. Sem. Univ. Hamburg 25, 36–61.Google Scholar
[31] Skellam, J. G. and Shenton, L. R. (1957) Distributions associated with random walk and recurrent events. J. R. Statist. Soc. B 19, 64–118.Google Scholar
[32] Smith, W. L. (1958) Renewal theory and its ramifications. J. R. Statist. Soc. B 20, 243–302.Google Scholar
[33] Smith, W. L. (1960) Infinitesimal renewal processes. Contributions to Probability and Statistics (ed. Olkin, I.) 396–413. Stanford.Google Scholar
[34] Takács, L. (1967) Combinatorial Methods in the Theory of Stochastic Processes. Wiley, New York.Google Scholar
[35] Taylor, S. J. (1973) Sample path properties of processes with stationary independent increments. Stochastic Geometry and Stochastic Analysis. Wiley, London.Google Scholar
[36] Widder, D. V. (1941) The Laplace Transform. Princeton. Note added in proof A further reference which has appeared since this paper was written, and which is very germane to these problems, is: Google Scholar
[37] Horowitz, J. (1972) Similinear Markov processes, subordinators and renewal theory. Z. Wahrscheinlichkeitsth. 24, 167–193.Google Scholar