Published online by Cambridge University Press: 01 July 2016
The systems considered are single-server, though the theory has wider application to models of adaptive queueing systems. Arrival and service mechanisms are governed by state (n)-dependent mean arrival and service rates λn and µn. It is assumed that the choice of λn and µn leads to a stable regime. Formulae are sought that provide easy means of computing statistics of effectiveness of systems. A measure of traffic intensity is first defined in terms of ‘effective’ service time and inter-arrival intervals. It is shown that the latter have a renewal type connection with appropriately defined mean effective arrival and service rates λ∗ and µ∗ and that in consequence the ratio λ∗/µ∗ is the traffic intensity, equal moreover to 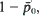 where
where 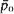 is the stable probability of an empty system, consistent with other systems. It is also shown that for first come, first served discipline the equivalent
is the stable probability of an empty system, consistent with other systems. It is also shown that for first come, first served discipline the equivalent 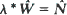 of Little's formula holds, where
of Little's formula holds, where 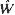 and
and 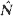 are the mean waiting time of an arrival and mean system size at an arbitrary epoch. In addition it appears that stable regime output intervals are statistically identical with effective inter-arrival intervals. Symmetrical moment formulae of arbitrary order are derived algebraically for effective inter-arrival and service intervals, for waiting time, for busy period and for output.
are the mean waiting time of an arrival and mean system size at an arbitrary epoch. In addition it appears that stable regime output intervals are statistically identical with effective inter-arrival intervals. Symmetrical moment formulae of arbitrary order are derived algebraically for effective inter-arrival and service intervals, for waiting time, for busy period and for output.