Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-25T23:59:56.733Z Has data issue: false hasContentIssue false
  • English
  • Français

Gaussian expansions and bounds for the Poisson distribution applied to the Erlang B formula

Part of: Asymptotic theory Special processes Distribution theory

Published online by Cambridge University Press:  01 July 2016

A. J. E. M. Janssen ,
J. S. H. van Leeuwaarden  and
B. Zwart
A. J. E. M. Janssen*
Affiliation:
Philips Research
J. S. H. van Leeuwaarden*
Affiliation:
Eindhoven University of Technology and EURANDOM
B. Zwart*
Affiliation:
Georgia Institute of Technology
*
∗ Postal address: Philips Research, Digital Signal Processing Group, HTC-36, 5656 AE Eindhoven, The Netherlands. Email address: [email protected]
∗∗ Postal address: EURANDOM, PO Box 513, 5600 MB Eindhoven, The Netherlands. Email address: [email protected]
∗∗∗ Postal address: Georgia Institute of Technology, H. Milton Stewart School of Industrial and Systems Engineering, 765 Ferst Drive, Atlanta, GA 30332, USA. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper presents new Gaussian approximations for the cumulative distribution function P(Aλ ≤ s) of a Poisson random variable Aλ with mean λ. Using an integral transformation, we first bring the Poisson distribution into quasi-Gaussian form, which permits evaluation in terms of the normal distribution function Φ. The quasi-Gaussian form contains an implicitly defined function y, which is closely related to the Lambert W-function. A detailed analysis of y leads to a powerful asymptotic expansion and sharp bounds on P(Aλ ≤ s). 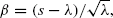The results for P(Aλ ≤ s) differ from most classical results related to the central limit theorem in that the leading term Φ(β), with is replaced by Φ(α), where α is a simple function of s that converges to β as s tends to ∞. Changing β into α turns out to increase precision for small and moderately large values of s. The results for P(Aλ ≤ s) lead to similar results related to the Erlang B formula. The asymptotic expansion for Erlang's B is shown to give rise to accurate approximations; the obtained bounds seem to be the sharpest in the literature thus far.

Keywords

Erlang B formulaErlang loss modelPoisson distributionnormal distributionGaussian integralsLambert W-functionRamanujan's conjectureasymptotic expansionbounds

MSC classification

Primary: 34E05: Asymptotic expansions 60K25: Queueing theory 62E20: Asymptotic distribution theory
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 40 , Issue 1 , March 2008 , pp. 122 - 143
Copyright
Copyright © Applied Probability Trust 2008 

References

Atar, R., Mandelbaum, A. and Shaikhet, G. (2006). Queueing systems with many servers: null controllability in heavy traffic. Ann. Appl. Prob. 16, 1764–1804.CrossRefGoogle Scholar
Barndorff-Nielsen, O. E. and Cox, D. R. (1990). Asymptotic Techniques for Use in Statistics. Chapman and Hall, London.Google Scholar
Bhattacharya, R. N. and Rao, R. R. (1976). Normal Approximations and Asymptotic Expansions. John Wiley, New York.Google Scholar
Borst, S., Mandelbaum, A. and Reiman, M. (2004). Dimensioning large call centers. Operat. Res. 52, 17–34.Google Scholar
Brockmeyer, E., Halstrøm, H. L. and Jensen, A. (1948). The life and works of A. K. Erlang. Trans. Danish Acad. Tech. Sci. 1948, 277pp.Google Scholar
Corless, R. M. et al. (1996). On the Lambert W-function. Adv. Comput. Math. 5, 329–359.CrossRefGoogle Scholar
Feller, W. (1966). An Introduction to Probability Theory and Its Applications, Vol. II. John Wiley, New York.Google Scholar
Flajolet, P., Grabner, P. J., Kirschenhofer, P. and Prodinger, H. (1995). On Ramanujan's Q-function. J. Comput. Appl. Math. 58, 103–116.Google Scholar
Gans, N., Koole, G. and Mandelbaum, A. (2003). Telephone call centers: tutorial, review and research prospects. Manufacturing Service Operat. Manag. 5, 79–141.CrossRefGoogle Scholar
Halfin, S. and Whitt, W. (1981). Heavy-traffic limits for queues with many exponential servers. Operat. Res. 29, 567–588.Google Scholar
Hwang, H. K. (1997). Asymptotic estimates of elementary probability distributions. Studies Appl. Math. 4, 339–417.Google Scholar
Jagerman, D. (1974). Some properties of the Erlang loss function. Bell System Tech. J. 53, 525–551.Google Scholar
Janssen, A. J. E. M., van Leeuwaarden, J. S. H. and Zwart, B. (2007). Corrected asymptotics for a multi-server queue in the Halfin–Whitt regime. Submitted.Google Scholar
Janssen, A. J. E. M., van Leeuwaarden, J. S. H. and Zwart, B. (2007). Corrected server staffing by expanding Erlang C. Submitted.Google Scholar
Jeffrey, D. J., Corless, R. M., Hare, D. E. G. and Knuth, D. E. (1995). Sur l'inversion de y α e y au moyen des nombres de Stirling associés. C. R. Acad. Sci. Paris 320, 1449–1452.Google Scholar
Johnson, N. L., Kotz, S. and Kemp, A. W. (1992). Univariate Discrete Distributions, 2nd edn. John Wiley, New York.Google Scholar
Kelly, F. P. (1991). Loss networks. Ann. Appl. Prob. 1, 319–378.Google Scholar
Michel, R. (1993). On Berry–Esseen bounds for the compound Poisson distribution. Insurance Math. Econom. 13, 35–37.CrossRefGoogle Scholar
Petrov, V. V. (1995). Limit Theorems of Probability Theory. Clarendon Press, Oxford.Google Scholar
Reed, J. (2006). The G/GI/N queue in the Halfin–Whitt regime. Submitted.Google Scholar
Temme, N. M. (1979). The asymptotic expansion of the incomplete gamma functions. SIAM J. Math. Anal. 10, 757–766.Google Scholar
Temme, N. M. (1992). Asymptotic inversion of incomplete gamma functions. Math. Comput. 58, 755–764.CrossRefGoogle Scholar
Temme, N. M. (1996). Special Functions. John Wiley, New York.Google Scholar