Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Quine, M. P.
and
Seneta, E.
1969.
A LIMIT THEOREM FOR THE GALTON‐WATSON PROCESS WITH IMMIGRATION.
Australian Journal of Statistics,
Vol. 11,
Issue. 3,
p.
166.
Athreya, Krishna B.
and
Ney, Peter
1970.
The local limit theorem and some related aspects of super-critical branching processes.
Transactions of the American Mathematical Society,
Vol. 152,
Issue. 1,
p.
233.
Darling, D. A.
1970.
The Galton-Watson process with infinite mean.
Journal of Applied Probability,
Vol. 7,
Issue. 2,
p.
455.
Quine, M. P.
1970.
The multi-type Galton-Watson process with immigration.
Journal of Applied Probability,
Vol. 7,
Issue. 2,
p.
411.
Darling, D. A.
1970.
The Galton-Watson process with infinite mean.
Journal of Applied Probability,
Vol. 7,
Issue. 02,
p.
455.
Seneta, E.
1970.
A note on the supercritical Galton-Watson process with immigration.
Mathematical Biosciences,
Vol. 6,
Issue. ,
p.
305.
Seneta, E.
1970.
An Explicit-Limit Theorem for the Critical Galton–Watson Process with Immigration.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 32,
Issue. 1,
p.
149.
Pakes, A. G.
1970.
An asymptotic result for a subcritical branching process with immigration.
Bulletin of the Australian Mathematical Society,
Vol. 2,
Issue. 2,
p.
223.
Seneta, E.
1970.
On invariant measures for simple branching processes (Summary).
Bulletin of the Australian Mathematical Society,
Vol. 2,
Issue. 3,
p.
359.
Fahady, K. S.
Quine, M. P.
and
Vere-Jones, D.
1971.
Heavy traffic approximations for the Galton-Watson process.
Advances in Applied Probability,
Vol. 3,
Issue. 2,
p.
282.
Serge Dubuc, M.
1971.
La densit� de la loi-limite d'un processus en cascade expansif.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 19,
Issue. 4,
p.
281.
Fahady, K. S.
Quine, M. P.
and
Vere-Jones, D.
1971.
Heavy traffic approximations for the Galton-Watson process.
Advances in Applied Probability,
Vol. 3,
Issue. 2,
p.
282.
Pakes, A. G.
1971.
Some limit theorems for the total progeny of a branching process.
Advances in Applied Probability,
Vol. 3,
Issue. 1,
p.
176.
Seneta, E.
1971.
On invariant measures for simple branching processes.
Journal of Applied Probability,
Vol. 8,
Issue. 1,
p.
43.
Pakes, A. G.
1971.
On a Theorem of Quine and Seneta for the Galton‐Watson Process With Immigration.
Australian Journal of Statistics,
Vol. 13,
Issue. 3,
p.
159.
Pakes, A. G.
1971.
A branching process with a state dependent immigration component.
Advances in Applied Probability,
Vol. 3,
Issue. 2,
p.
301.
Pakes, A. G.
1971.
Branching processes with immigration.
Journal of Applied Probability,
Vol. 8,
Issue. 1,
p.
32.
Pakes, A. G.
1971.
Branching processes with immigration.
Journal of Applied Probability,
Vol. 8,
Issue. 01,
p.
32.
Heyde, C. C.
1971.
Some central limit analogues for supercritical Galton-Watson processes.
Journal of Applied Probability,
Vol. 8,
Issue. 1,
p.
52.
Pakes, A. G.
1972.
Further results on the critical Galton-Watson process with immigration.
Journal of the Australian Mathematical Society,
Vol. 13,
Issue. 3,
p.
277.
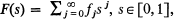 denote the probability generating function of the offspring distribution of a single individual. Our fundamental assumption, which holds throughout the sequel, is that fj ≠ 1, j = 0,1,2, …; in particular circumstances it shall be necessary to strengthen this to 0 < f0 ≡ F(0) < 1, which is the relevant assumption when extinction behaviour is to be considered. (Even so, our assumptions will always differ slightly from those of Harris (1963), p. 5.)
denote the probability generating function of the offspring distribution of a single individual. Our fundamental assumption, which holds throughout the sequel, is that fj ≠ 1, j = 0,1,2, …; in particular circumstances it shall be necessary to strengthen this to 0 < f0 ≡ F(0) < 1, which is the relevant assumption when extinction behaviour is to be considered. (Even so, our assumptions will always differ slightly from those of Harris (1963), p. 5.)