Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T16:54:11.287Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact Formulae for Variances of Functionals of Convex Hulls

Part of: General convexity Geometric probability and stochastic geometry

Published online by Cambridge University Press:  04 January 2016

Christian Buchta
Christian Buchta*
Affiliation:
Salzburg University
*
∗ Postal address: Department of Mathematics, Salzburg University, Hellbrunner Straße 34, 5020 Salzburg, Austria. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The vertices of the convex hull of a uniform sample from the interior of a convex polygon are known to be concentrated close to the vertices of the polygon. Furthermore, the remaining area of the polygon outside of the convex hull is concentrated close to the vertices of the polygon. In order to see what happens in a corner of the polygon given by two adjacent edges, we consider—in view of affine invariance—n points P1,…, Pn distributed independently and uniformly in the interior of the triangle with vertices (0, 1), (0, 0), and (1, 0). The number of vertices of the convex hull, which are close to the origin (0, 0), is then given by the number Ñn of points among P1,…, Pn, which are vertices of the convex hull of (0, 1), P1,…, Pn, and (1, 0). Correspondingly, D̃n is defined as the remaining area of the triangle outside of this convex hull. We derive exact (nonasymptotic) formulae for var Ñn and var 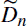. These formulae are in line with asymptotic distribution results in Groeneboom (1988), Nagaev and Khamdamov (1991), and Groeneboom (2012), as well as with recent results in Pardon (2011), (2012).

Keywords

Convex hullrandom pointvariance

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry
Secondary: 52A22: Random convex sets and integral geometry
Type
Stochastic Geometry and Statistical Applications
Information
Advances in Applied Probability , Volume 45 , Issue 4 , December 2013 , pp. 917 - 924
Copyright
© Applied Probability Trust 

References

Bárány, I. and Buchta, C. (1993). Random polytopes in a convex polytope, independence of shape, and concentration of vertices. Math. Ann. 297, 467–497.CrossRefGoogle Scholar
Bárány, I. and Reitzner, M. (2010). On the variance of random polytopes. Adv. Math. 225, 1986–2001.CrossRefGoogle Scholar
Bárány, I. and Steiger, W. (2013). On the variance of random polygons. Comput. Geom. 46, 173–180.CrossRefGoogle Scholar
Buchta, C. (1984). Stochastische Approximation konvexer Polygone. Z. Wahrscheinlichkeitsth. 67, 283–304.CrossRefGoogle Scholar
Buchta, C. (2003). On the distribution of the number of vertices of a random polygon. Anz. Österreich. Akad. Wiss. Math.-Natur. Kl. 139, 17–19.Google Scholar
Buchta, C. (2005). An identity relating moments of functionals of convex hulls. Discrete Comput. Geom. 33, 125–142.CrossRefGoogle Scholar
Buchta, C. (2006). The exact distribution of the number of vertices of a random convex chain. Mathematika 53, 247–254.CrossRefGoogle Scholar
Buchta, C. (2009). On the number of vertices of the convex hull of random points in a square and a triangle. Anz. Österreich. Akad. Wiss. Math.-Natur. Kl. 143, 3–10.Google Scholar
Buchta, C. (2012). On the boundary structure of the convex hull of random points. Adv. Geom. 12, 179–190.CrossRefGoogle Scholar
Buchta, C. and Reitzner, M. (1997). Equiaffine inner parallel curves of a plane convex body and the convex hulls of randomly chosen points. Prob. Theory Relat. Fields 108, 385–415.CrossRefGoogle Scholar
Buchta, C. and Reitzner, M. (2001). The convex hull of random points in a tetrahedron: Solution of Blaschke's problem and more general results. J. Reine Angew. Math. 536, 1–29.CrossRefGoogle Scholar
Cabo, A. J. and Groeneboom, P. (1994). Limit theorems for functionals of convex hulls. Prob. Theory Relat. Fields 100, 31–55.CrossRefGoogle Scholar
Efron, B. (1965). The convex hull of a random set of points. Biometrika 52, 331–343.CrossRefGoogle Scholar
Groeneboom, P. (1988). Limit theorems for convex hulls. Prob. Theory Relat. Fields 79, 327–368.CrossRefGoogle Scholar
Groeneboom, P. (2012). Convex hulls of uniform samples from a convex polygon. Adv. Appl. Prob. 44, 330–342.CrossRefGoogle Scholar
Jewell, N. P. and Romano, J. P. (1982). Coverage problems and random convex hulls. J. Appl. Prob. 19, 546–561.CrossRefGoogle Scholar
Jewell, N. P. and Romano, J. P. (1985). Evaluating inclusion functionals for random convex hulls. Z. Wahrscheinlichkeitsth. 68, 415–424.CrossRefGoogle Scholar
Nagaev, A. V. (1995). Some properties of convex hulls generated by homogeneous Poisson point processes in an unbounded convex domain. Ann. Inst. Statist. Math. 47, 21–29.CrossRefGoogle Scholar
Nagaev, A. V. and Khamdamov, I. M. (1991). Limit theorems for functionals of random convex hulls. Preprint, Institute of Mathematics, Academy of Sciences of Uzbekistan, Tashkent (in Russian).Google Scholar
Pardon, J. (2011). Central limit theorems for random polygons in an arbitrary convex set. Ann. Prob. 39, 881–903.CrossRefGoogle Scholar
Pardon, J. (2012). Central limit theorems for uniform model random polygons. J. Theoret. Prob. 25, 823–833.CrossRefGoogle Scholar
Reitzner, M. (2010). Random polytopes. In New Perspectives in Stochastic Geometry, Oxford University Press, pp. 45–76.Google Scholar
Rényi, A. and Sulanke, R. (1963). Über die konvexe Hülle von n zufällig gewählten Punkten. Z. Wahrscheinlichkeitsth. 2, 75–84.CrossRefGoogle Scholar
Rényi, A. and Sulanke, R. (1964). Über die konvexe Hülle von n zufällig gewählten Punkten. II. Z. Wahrscheinlichkeitsth. 3, 138–147.CrossRefGoogle Scholar
Schneider, C. (2007). Symbolic summation assists combinatorics. Sém. Lothar. Combin. 56, 1–36.Google Scholar
Schneider, R. (2008). Recent results on random polytopes. Boll. Unione Mat. Ital. (9) 1, 17–39.Google Scholar
Schneider, R. and Weil, W. (2008). Stochastic and Integral Geometry. Springer, Berlin.CrossRefGoogle Scholar
Schreiber, T. and Yukich, J. E. (2008). Variance asymptotics and central limit theorems for generalized growth processes with applications to convex hulls and maximal points. Ann. Prob. 36, 363–396.CrossRefGoogle Scholar