Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kendall, David G.
1986.
The Craft of Probabilistic Modelling.
Vol. 1,
Issue. ,
p.
3.
Le, Hui-Lin
1987.
Explicit formulae for polygonally generated shape-densities in the basic tile.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 101,
Issue. 2,
p.
313.
Le, Hui-Lin
1987.
Singularities of convex-polygonally generated shape-densities.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 102,
Issue. 3,
p.
587.
Clifford, Peter
Green, N. J. B.
and
Pilling, M. J.
1987.
Statistical Models of Chemical Kinetics in Liquids.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 49,
Issue. 3,
p.
266.
Kendall, David G.
1987.
Further Developments and Applications of the Statistical Theory of Shape.
Theory of Probability & Its Applications,
Vol. 31,
Issue. 3,
p.
407.
Ripley, B. D.
1988.
Quantitative Analysis of Mineral and Energy Resources.
p.
301.
Mannion, David
1988.
A Markov chain of triangle shapes.
Advances in Applied Probability,
Vol. 20,
Issue. 2,
p.
348.
Itoh, Yoshiaki
1989.
A certain configuration of random points on a circle associated with a generalized Lotka-Volterra equation.
Journal of Applied Probability,
Vol. 26,
Issue. 04,
p.
898.
Kendall, David G.
1990.
Random delaunay simplexes in m.
Journal of Statistical Planning and Inference,
Vol. 25,
Issue. 3,
p.
225.
Mannion, David
1990.
Convergence to collinearity of a sequence of random triangle shapes.
Advances in Applied Probability,
Vol. 22,
Issue. 4,
p.
831.
Mannion, David
1990.
The invariant distribution of a sequence of random collinear triangle shapes.
Advances in Applied Probability,
Vol. 22,
Issue. 4,
p.
845.
Croft, Hallard T.
Falconer, Kenneth J.
and
Guy, Richard K.
1991.
Unsolved Problems in Geometry.
Vol. 2,
Issue. ,
p.
48.
Goodall, Colin
1991.
Procrustes Methods in the Statistical Analysis of Shape.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 53,
Issue. 2,
p.
285.
Gates, John
1993.
Some Dual Problems of Geometric Probability in the Plane.
Combinatorics, Probability and Computing,
Vol. 2,
Issue. 1,
p.
11.
Bavaud, François
1994.
Triangular dynamics under pressure.
Journal of Statistical Physics,
Vol. 76,
Issue. 1-2,
p.
645.
Gates, John
1994.
Shape distributions for planar triangles by dual construction.
Advances in Applied Probability,
Vol. 26,
Issue. 2,
p.
324.
Slice, Dennis E.
1996.
Advances in Morphometrics.
p.
113.
Kendall, Wilfrid S.
1998.
A diffusion model for bookstein triangle shape.
Advances in Applied Probability,
Vol. 30,
Issue. 2,
p.
317.
Letac, Gérard
and
Scarsini, Marco
1998.
Random nested tetrahedra.
Advances in Applied Probability,
Vol. 30,
Issue. 3,
p.
619.
Tang, Carol M.
and
Roopnarine, Peter D.
2003.
Complex Morphological Variability in Complex Evaporitic Systems: Thermal Spring Snails from the Chihuahuan Desert, Mexico.
Astrobiology,
Vol. 3,
Issue. 3,
p.
597.
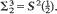 . A new formula is given for the shape-density for a triangle whose vertices are i.i.d.-uniform in a compact convex set K, and an exact evaluation of that shape-density is obtained when K is a circular disk. An (x, y)-diagram for an auxiliary shape-density
. A new formula is given for the shape-density for a triangle whose vertices are i.i.d.-uniform in a compact convex set K, and an exact evaluation of that shape-density is obtained when K is a circular disk. An (x, y)-diagram for an auxiliary shape-density 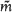 is then introduced. When K = circular disk, it is shown that
is then introduced. When K = circular disk, it is shown that 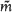 is virtually constant over a substantial region adjacent to the relevant section of the collinearity locus, large enough to contain the work-space for most collinearity studies, and particularly appropriate when the ‘strip’ method is used to assess near-collinearity.
is virtually constant over a substantial region adjacent to the relevant section of the collinearity locus, large enough to contain the work-space for most collinearity studies, and particularly appropriate when the ‘strip’ method is used to assess near-collinearity.

