Suppose, to take a simple example, we have a set of sibships. Each individual (sib) has a certain measured character x. We wish to estimate the interclass (or sib–sib) correlation for this character. Our model is as follows. In sibship s the observed values x are supposed drawn from a distribution with (true) mean ms and variance vs. The sibships are drawn from a population of sibships, so that the ms have a mean M and variance B, and the vs have mean A. (We also suppose that the number ns of sibs in sibship s is independent of ms and vs.) The interclass correlation is then easily seen to be

ρ = B/(A + B).

The obvious way to proceed is to estimate A and B first, and then find ρ. Take a sample of k sibships. In sibship s the observed mean is 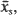and the deviance (sum of squares of deviations) δs. Let n = σ ns = the total number of individuals in the sample, and δ = σ δs = the total deviance within sibships. Proceed iteratively as follows: