Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T09:59:50.540Z Has data issue: false hasContentIssue false
  • English
  • Français

Entropy inequalities for classes of probability distributions I. The univariate case

Published online by Cambridge University Press:  01 July 2016

Samuel Karlin  and
Yosef Rinott
Samuel Karlin*
Affiliation:
Stanford University
Yosef Rinott*
Affiliation:
Stanford University
*
∗Postal address: Department of Mathematics, Stanford University, Stanford CA 94305, U.S.A.
∗Postal address: Department of Mathematics, Stanford University, Stanford CA 94305, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

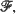Entropy functionals of probability densities feature importantly in classifying certain finite-state stationary stochastic processes, in discriminating among competing hypotheses, in characterizing Gaussian, Poisson, and other densities, in describing information processes, and in other contexts. Two general types of problems are considered. For a given parametric family of densities the member of maximal (or sometimes minimal) entropy is ascertained. Secondly, we determine a natural (partial) ordering over 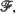for which the entropy functional is monotone. The examples include the multiparameter binomial, multiparameter negative binomial, some classes of log concave densities, and others.

Keywords

ENTROPY FUNCTIONALMAJORIZATION ORDERINGTOTAL POSITIVITYLOG CONCAVITY
Type
Research Article
Information
Advances in Applied Probability , Volume 13 , Issue 1 , March 1981 , pp. 93 - 112
Copyright
Copyright © Applied Probability Trust 1981 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Yosef Rinott is also a member of the Department of Statistics, The Hebrew University, Jerusalem, Israel.

Supported in part by NIH Grant 2R01 GM10452-16 and NSF Grant MCS 76-80624-A02.

References

Eaton, M. L. and Perlman, M. D. (1977) Reflection groups, generalized Schur functions and the geometry of majorization. Ann. Prob. 5, 829–860.Google Scholar
Fan, K. and Lorentz, G. G. (1954) An integral inequality. Amer. Math. Monthly 61, 626–631.Google Scholar
Guiasu, S. (1977) Information Theory with Applications. McGraw-Hill, New York.Google Scholar
Hardy, G. H., Littlewood, J. E. and Pólya, G. (1934) Inequalities. Cambridge University Press.Google Scholar
Karlin, S. (1968). Total Positivity. Stanford University Press.Google Scholar
Karlin, S. and Bradt, R. (1956). On the design and comparison of certain dichotomous experiments. Ann. Math. Statist. 27, 390–409.Google Scholar
Karlin, S. and Novikoff, A. (1963) Generalized convex inequalities. Pacific J. Math. 13, 1251–1279.Google Scholar
Karlin, S. and Rinott, Y. (1981) Entropy inequalities for classes of probability distributions, II. The multivariate case. Adv. Appl. Prob. 13(2).Google Scholar
Karlin, S. and Studden, W. J. (1966) Tchebycheff Systems: With Applications in Analysis and Statistics. Interscience, New York.Google Scholar
Kullback, S. (1959) Information Theory and Statistics. Wiley, New York.Google Scholar
Lindström, B. (1975) Determining subsets by unramified experiments. In A Survey of Statistical Design and Linear Models, North-Holland, Amsterdam, 407–418.Google Scholar
Marshall, A. W. and Olkin, I. (1979) Inequalities, Theory of Majorization and Its Application. Academic Press, New York.Google Scholar
Mateev, P. (1978) On the entropy of multinomial distributions. Theory Prob. Appl. 23, 188–190.Google Scholar
Mudholkar, G. S. (1966) The integral of an invariant unimodal function over an invariant convex set—an inequality and applications. Proc. Amer. Math. Soc. 17, 1327–1333.Google Scholar
Ostrowski, A. (1952) Sur quelques applications des fonctions convexes et concaves au sens de I. Schur. J. Math. Pures Appl. 31, 253–292.Google Scholar
Pólya, G. and Szegö, G. (1925) Aufgaben and Lehrsatze aus der Analysis. Berlin.Google Scholar
Rao, C. R. (1973) Linear Statistical Inference and Its Applications, 2nd edn. Wiley, New York.CrossRefGoogle Scholar
Rényi, A. (1961) On measures of entropy and information. Proc. 4th Berkeley Symp. Math. Statist. Prob. 1, 541–561.Google Scholar
Rinott, Y. (1973) Multivariate majorization and rearrangement inequalities with some applications in probability and statistics. Israel J. Math. 15, 60–77.Google Scholar
Shepp, L. A. and Olkin, I. (1978) Entropy of the sum of independent Bernoulli random variables and of the multinomial distribution. Tech. Report. No. 131, Dept. of Statistics, Stanford University.Google Scholar