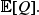Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T18:18:50.111Z Has data issue: false hasContentIssue false
  • English
  • Français

Endemic Behaviour of SIS Epidemics with General Infectious Period Distributions

Part of: Stochastic processes

Published online by Cambridge University Press:  22 February 2016

Peter Neal
Peter Neal*
Affiliation:
Lancaster University
*
∗ Postal address: Department of Mathematics and Statistics, Fylde College, Lancaster University, Lancaster LA1 4YF, UK. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the endemic behaviour of a homogeneously mixing SIS epidemic in a population of size N with a general infectious period, Q, by introducing a novel subcritical branching process with immigration approximation. This provides a simple but useful approximation of the quasistationary distribution of the SIS epidemic for finite N and the asymptotic Gaussian limit for the endemic equilibrium as N → ∞. A surprising observation is that the quasistationary distribution of the SIS epidemic model depends on Q only through

Keywords

SIS epidemicbranching process with immigrationGaussian processquasistationary distribution

MSC classification

Primary: 92D30: Epidemiology
Secondary: 60G10: Stationary processes
Type
Research Article
Information
Advances in Applied Probability , Volume 46 , Issue 1 , March 2014 , pp. 241 - 255
Copyright
© Applied Probability Trust 

References

Aldous, D. (1978). Stopping times and tightness. Ann. Prob. 6, 335–340.Google Scholar
Andersson, H. and Britton, T. (2000). Stochastic epidemics in dynamic populations: quasi-stationarity and extinction. J. Math. Biol. 41, 559–580.CrossRefGoogle Scholar
Andersson, H. and Djehiche, B. (1998). A threshold limit theorem for the stochastic logistic epidemic. J. Appl. Prob. 35, 662–670.Google Scholar
Arrigoni, F. and Pugliese, A. (2007). Global stability of equilibria for a metapopulation S-I-S model. In Math Everywhere, Springer, Berlin, pp. 229–240.Google Scholar
Ball, F. (1999). Stochastic and deterministic models for SIS epidemics among a population partitioned into households. Math. Biosci. 156, 41–67.CrossRefGoogle ScholarPubMed
Ball, F. and Donnelly, P. (1995). Strong approximations for epidemic models. Stoch. Process. Appl. 55, 1–21.Google Scholar
Billingsley, P. (1968). Convergence of Probability Measures. John Wiley, New York.Google Scholar
Britton, T. and Neal, P. (2010). The time to extinction for a stochastic SIS-household-epidemic model. J. Math. Biol. 61, 763–779.CrossRefGoogle ScholarPubMed
Clancy, D. (2012). Approximating quasistationary distributions of birth–death processes. J. Appl. Prob. 49, 1036–1051.Google Scholar
Clancy, D. and Mendy, S. T. (2011). Approximating the quasistationary distribution of the SIS model for endemic infection. Methodol. Comput. Appl. Prob. 13, 603–618.CrossRefGoogle Scholar
Clancy, D. and Pollett, P. K. (2003). A note on quasistationary distributions of birth–death processes and the SIS logistic epidemic. J. Appl. Prob. 40, 821–825.Google Scholar
Ghoshal, G., Sander, L. M. and Sokolov, I. M. (2004). SIS epidemics with household structure: the self-consistent field method. Math. Biosci. 190, 71–85.CrossRefGoogle ScholarPubMed
Kryscio, R. and Lefèvre, C. (1989). On the extinction of the S-I-S stochastic logistic epidemic. J. Appl. Prob. 26, 685–694.Google Scholar
Kurtz, T. G. (1971). Limit theorems for sequences of Jump Markov processes approximating ordinary differential processes. J. Appl. Prob. 8, 344–356.Google Scholar
Lindvall, T. (1973). Weak convergence of probability measures and random functions in function space on D(0, ∞). J. Appl. Prob. 10, 109–121.Google Scholar
Nåsell, I. (1996). The quasistationary distribution of the closed endemic SIS model. Adv. Appl. Prob. 28, 895–932.Google Scholar
Nåsell, I. (1999a). On the quasistationary distribution of the stochastic logistic epidemic. Math. Biosci. 156, 21–40.Google Scholar
Nåsell, I. (1999b). On the time to extinction in recurrent epidemics. J. R. Statist. Soc. B 61, 309–330.CrossRefGoogle Scholar
Nåsell, I. (2003). An extension of the moment closure method. Theoret. Pop. Biol. 64, 233–239.Google Scholar
Neal, P. (2006). Stochastic and deterministic analysis of SIS household epidemics. Adv. Appl. Prob. 38, 943–968. (Correction: 44 (2012), 309–310.)Google Scholar
Neal, P. (2008). The SIS great circle epidemic model. J. Appl. Prob. 45, 513–530.Google Scholar
Rogers, L. C. G. and Williams, D. (1994). Diffusions, Markov Processes, and Martingales, Vol. 1, Foundations. 2nd edn. John Wiley, Chichester.Google Scholar
Scalia-Tomba, G. (1990). On the asymptotic final size distribution of epidemics in heterogeneous populations. In Stochastic Processes in Epidemic Theory, Springer, New York., pp. 189–196.CrossRefGoogle Scholar
Weiss, G. H. and Dishon, M. (1971). On the asymptotic behavior of the stochastic and deterministic models of an epidemic. Math. Biosci. 11, 261–265.Google Scholar