Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-22T19:54:57.053Z Has data issue: false hasContentIssue false
  • English
  • Français

Distribution properties of the system failure time in a general shock model

Published online by Cambridge University Press:  01 July 2016

J. G. Shanthikumar  and
Ushio Sumita
J. G. Shanthikumar*
Affiliation:
University of Arizona
Ushio Sumita*
Affiliation:
University of Rochester
*
∗Postal address: Systems and Industrial Engineering Department, University of Arizona, Tucson, AZ 85721, U.S.A.
∗∗ Postal address: The Graduate School of Management, The University of Rochester, Rochester, NY 14627, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

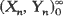In this paper we study some distribution properties of the system failure time in general shock models associated with correlated renewal sequences (Xn, Yn) . Two models, depending on whether the magnitude of the nth shock Xn is correlated to the length Yn of the interval since the last shock, or to the length of the subsequent interval to the next shock, are considered. Sufficient conditions under which the system failure time is completely monotone, new better than used, new better than used in expectation, and harmonic new better than used in expectation are given for these two models.

Keywords

CORRELATED RENEWAL PROCESSCOMPLETE MONOTONICITYNEW BETTER THAN USEDNEW BETTER THAN USED IN EXPECTATIONHARMONIC NEW BETTER THAN USED IN EXPECTATION
Type
Research Article
Information
Advances in Applied Probability , Volume 16 , Issue 2 , June 1984 , pp. 363 - 377
Copyright
Copyright © Applied Probability Trust 1984 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] A-Hameed, M. S. and Proschan, F. (1973) Nonstationary shock models. Stoch. Proc. Appl. 1, 383–404.Google Scholar
[2] A-Hameed, M. S. and Proschan, F. (1975) Shock models with underlying birth processes. J. Appl. Prob. 12, 18–28.CrossRefGoogle Scholar
[3] Barlow, R. E. and Proschan, F. (1975) Statistical Theory of Reliability and Life Testing–Probability Models. Holt, Rinehart and Winston, New York.Google Scholar
[4] Block, H. W. and Savtts, T. H. (1978) Shock models with NBUE survival. J. Appl. Prob. 15, 621–628.Google Scholar
[5] Esary, J. D., Marshall, A. W. and Proschan, F. (1973) Shock models and wear processes. Ann. Prob. 1, 627–649.Google Scholar
[6] Feller, W. (1966) An Introduction to Probability Theory and its Applications, Vol. 2. Wiley, New York.Google Scholar
[7] Ghosh, M. and Ebrahimi, N. (1982) Shock models leading to increased failure rate and decreasing mean residual life survival. J. Appl. Prob. 19, 158–166.Google Scholar
[8] Karlin, S. (1968) Total Positivity. Stanford University Press, Stanford, CA.Google Scholar
[9] Keilson, J. (1979) Markov Chain Models–Rarity and Exponentiality. Springer-Verlag, New York.CrossRefGoogle Scholar
[10] Klefsjö, B. (1981) HNBUE survival under some shock models. Scand. J. Statist. 8, 39–47.Google Scholar
[11] Klefsjö, B. (1982) The HNBUE and HNWUE classes of life distributions. Naval Res. Logist. Quart. 29, 331–344.Google Scholar
[12] Marshall, A. W. and Proschan, F. (1970) Mean life of series and parallel systems. J. Appl. Prob. 7, 165–174.Google Scholar
[13] Marshall, A. W. and Shaked, M. (1983) New better than used processes. Adv. Appl. Prob. 15, 601–615.Google Scholar
[14] Rolski, T. (1975) Mean residual life. Bull. Internat. Statist. Inst. 46, 266–270.Google Scholar
[15] Ross, S. M. (1981) Generalized Poisson shock models. Ann. Prob. 9, 896–898.Google Scholar
[16] Shanthikumar, J. G. and Sumita, U. (1983) General shock models associated with correlated renewal sequences. J. Appl. Prob. 20, 600–614.CrossRefGoogle Scholar
[17] Widder, D. V. (1946) The Laplace Transform. Princeton University Press, Princeton, NJ.Google Scholar