No CrossRef data available.
Published online by Cambridge University Press: 01 July 2016
Aggregated spatial patterns may be generated by a clustering process (see, for example, Bartlett (1964)) in which ‘parent’ events are distributed completely at random, and produce, independently, random numbers of ‘offspring’ according to some distribution Pn; the position of each offspring relative to its parent is governed, independently, by a given bivariate distribution. Parents and offspring are assumed indistinguishable. For such a process, Bartlett (1974) shows that the distribution function F of the distance, X say, from a randomly selected point to the nearest event is given by
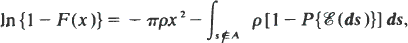 where ρ denotes the mean number of parents per unit area, A is the circle with centre the origin and radius x, and E(ds) denotes the event ‘no offspring in A from parent in ds’.
where ρ denotes the mean number of parents per unit area, A is the circle with centre the origin and radius x, and E(ds) denotes the event ‘no offspring in A from parent in ds’.