Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T00:58:30.061Z Has data issue: false hasContentIssue false
  • English
  • Français

Dispersive ordering results

Published online by Cambridge University Press:  01 July 2016

James Lynch ,
Gillian Mimmack  and
Frank Proschan
James Lynch*
Affiliation:
Florida State University
Gillian Mimmack
Affiliation:
Florida State University
Frank Proschan
Affiliation:
Florida State University
*
∗Permanent address: Department of Statistics, Pennsylvania State University, University Park, PA 16802, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A distribution F is less dispersed than a distribution G if for all .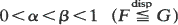

We generalize a characterization of dispersive ordering of Shaked (1982) concerning sign changes of Fc – G, where Fc is a translate of F. We then use this generalization plus total positivity to develop a simple proof of a characterization of dispersive distributions due to Lewis and Thompson (1981); a distribution H is dispersive if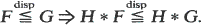

Type
Letters to the Editor
Information
Advances in Applied Probability , Volume 15 , Issue 4 , December 1983 , pp. 889 - 891
Copyright
Copyright © Applied Probability Trust 1983 

Footnotes

Research supported under Grant DAAG 29-82-K-0168 with the US Army Research Office.

†Postal address: Department of Statistics and Statistical Consulting Center, The Florida State University, Tallahassee, FL 32306, U.S.A.

Research supported under Contract AFOSR-82-K-0007 with the Air Force Office of Scientific Research, AFSC, USAF.

References

Ibragimov, I. A. (1956). On the composition of unimodal distributions. Theory Prob. Appl. 1, 255–260.CrossRefGoogle Scholar
Karlin, S. (1968). Total Positivity, Vol. 1. Stanford University Press.Google Scholar
Lewis, T. and Thompson, J. W. (1981). Dispersive distributions, and the connection between dispersivity and strong unimodality. J. Appl. Prob. 18, 76–90.CrossRefGoogle Scholar
Shaked, M. (1982). Dispersive ordering of distributions. J. Appl. Prob. 19, 310–320.CrossRefGoogle Scholar