Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Grimmett, Geoffrey
and
Kesten, Harry
1984.
First-passage percolation, network flows and electrical resistances.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 66,
Issue. 3,
p.
335.
Higuchi, Yasunari
1986.
A percolation problem for {±1}-valued strongly mixing random fields on ℤ
d
⋆
.
Probability Theory and Related Fields,
Vol. 73,
Issue. 4,
p.
597.
Aizenman, M.
Chayes, J. T.
Chayes, L.
and
Newman, C. M.
1988.
Discontinuity of the magnetization in one-dimensional 1/�x?y�2 Ising and Potts models.
Journal of Statistical Physics,
Vol. 50,
Issue. 1-2,
p.
1.
Grimmett, Geoffrey
1989.
Percolation.
p.
82.
Falconer, K. J.
and
Grimmett, G. R.
1992.
On the geometry of random Cantor sets and fractal percolation.
Journal of Theoretical Probability,
Vol. 5,
Issue. 3,
p.
465.
Häggström, Olle
and
Mester, Péter
2009.
Some two-dimensional finite energy percolation processes.
Electronic Communications in Probability,
Vol. 14,
Issue. none,
Alves, Rogério G.
Procacci, Aldo
and
Sanchis, Remy
2012.
Percolation on Infinite Graphs and Isoperimetric Inequalities.
Journal of Statistical Physics,
Vol. 149,
Issue. 5,
p.
831.


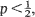 let
let