No CrossRef data available.
Published online by Cambridge University Press: 13 September 2022
We consider a sequence of Poisson cluster point processes on
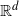 $\mathbb{R}^d$
: at step
$\mathbb{R}^d$
: at step
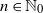 $n\in\mathbb{N}_0$
of the construction, the cluster centers have intensity
$n\in\mathbb{N}_0$
of the construction, the cluster centers have intensity
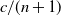 $c/(n+1)$
for some
$c/(n+1)$
for some
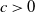 $c>0$
, and each cluster consists of the particles of a branching random walk up to generation n—generated by a point process with mean 1. We show that this ‘critical cluster cascade’ converges weakly, and that either the limit point process equals the void process (extinction), or it has the same intensity c as the critical cluster cascade (persistence). We obtain persistence if and only if the Palm version of the outgrown critical branching random walk is locally almost surely finite. This result allows us to give numerous examples for persistent critical cluster cascades.
$c>0$
, and each cluster consists of the particles of a branching random walk up to generation n—generated by a point process with mean 1. We show that this ‘critical cluster cascade’ converges weakly, and that either the limit point process equals the void process (extinction), or it has the same intensity c as the critical cluster cascade (persistence). We obtain persistence if and only if the Palm version of the outgrown critical branching random walk is locally almost surely finite. This result allows us to give numerous examples for persistent critical cluster cascades.