Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-11T15:47:48.675Z Has data issue: false hasContentIssue false
  • English
  • Français

The coupling of regenerative processes

Published online by Cambridge University Press:  01 July 2016

Hermann Thorisson
Hermann Thorisson*
Affiliation:
University of Göteborg
*
∗Postal address: Department of Mathematics, Chalmers University of Technology and University of Göteborg, S-412 96 Göteborg, Sweden. Supported in part by the Swedish Natural Science Research Council.
Get access Rights & Permissions [Opens in a new window]

Abstract

A distributional coupling concept is defined for continuous-time stochastic processes on a general state space and applied to processes having a certain non-time-homogeneous regeneration property: regeneration occurs at random times So, S1, · ·· forming an increasing Markov chain, the post-Sn process is conditionally independent of So, · ··, Sn–1 given Sn, and the conditional distribution is independent of n. 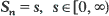The coupling problem is reduced to an investigation of the regeneration times So, S1, · ··, and a successful coupling is constructed under the condition that the recurrence times Xn+1 = Sn+1 – Sn given that , are stochastically dominated by an integrable random variable, and that the distributions 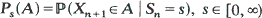, have a common component which is absolutely continuous with respect to Lebesgue measure (or aperiodic when the Sn's are lattice-valued). This yields results on the tendency to forget initial conditions as time tends to ∞. In particular, tendency towards equilibrium is obtained, provided the post-Sn process is independent of Sn. The ergodic results cover convergence and uniform convergence of distributions and mean measures in total variation norm. Rate results are also obtained under moment conditions on the Ps's and the times of the first regeneration.

Keywords

RENEWAL PROCESS: MARKOV CHAINREGENERATIVE RANDOM MEASURETIME-DEPENDENCE
Type
Research Article
Information
Advances in Applied Probability , Volume 15 , Issue 3 , September 1983 , pp. 531 - 561
Copyright
Copyright © Applied Probability Trust 1983 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Asmussen, S. (1979) Regenerative Processes. Lecture Notes, Institute of Mathematical Statistics, University of Copenhagen.Google Scholar
[2] Athreya, K. B. and Ney, P. (1978) A new approach to the limit theory of recurrent Markov chains. Trans. Amer. Math. Soc. 245, 493–501.CrossRefGoogle Scholar
[3] Doeblin, W. (1938) Exposé de la theorie des chaînes simple constantes de Markov à un nombre fini d'états. Rev. Math. Union Interbalkan. 2, 77–105.Google Scholar
[4] Feller, W. (1966) An Introduction to Probability Theory and its Applications. Wiley, New York.Google Scholar
[5] Garsia, A. M. (1973) On a convex function inequality for martingales. Ann. Prob. 1, 171–174.CrossRefGoogle Scholar
[6] Griffeath, D. (1975) A maximal coupling for Markov chains. Z. Wahrscheinlichkeitsth. 31, 95–106.CrossRefGoogle Scholar
[7] Griffeath, D. (1978) Coupling methods for Markov processes. Studies in Probability and Ergodic Theory. Adv. Math. Supplementary Studies 2.Google Scholar
[8] Jagers, P. (1974) Aspects of random measures and point processes. In Advances in Probability 3, ed. Ney, P. and Port, S., Dekker, New York, 179–239.Google Scholar
[9] Lindvall, T. (1979) On coupling of discrete renewal processes. Z. Wahrscheinlichkeitsth. 48, 57–70.CrossRefGoogle Scholar
[10] Lindvall, T. (1982) On coupling of continuous time renewal processes. J. Appl. Prob. 19, 82–89.CrossRefGoogle Scholar
[11] Miller, D. R. (1972) Existence of limits in regenerative processes. Ann. Math. Statist. 43, 1275–1282.CrossRefGoogle Scholar
[12] Neveu, J. (1975) Discrete-Parameter Martingales. North-Holland, Amsterdam.Google Scholar
[13] Ney, P. (1981) A refinement of the coupling method in renewal theory. Stoch. Proc. Appl. 11, 11–26.CrossRefGoogle Scholar
[14] Nummelin, E. (1978) A splitting technique for Harris recurrent Markov chains. Z. Wahrscheinlichkeitsth. 43, 309–318.CrossRefGoogle Scholar
[15] Pitman, J. W. and Speed, T. P. (1973) A note on random times. Stoch. Proc. Appl. 1, 369–374.CrossRefGoogle Scholar
[16] Pitman, J. W. (1974) Uniform rates of convergence for Markov chain transition probabilities. Z. Wahrscheinlichkeitsth. 29, 193–227.CrossRefGoogle Scholar
[17] Smith, W. L. (1955) Regenerative stochastic processes. Proc. R. Soc. London A 232, 6–31.Google Scholar
[18] Stone, C. and Wainger, S. (1967) One-sided error estimates in renewal theory. J. Analyse Math. XX, 325–352.CrossRefGoogle Scholar
[19] Thorisson, H. (1981) The Coupling of Regenerative Processes. , Department of Mathematics, Göteborg.Google Scholar
[20] Thorisson, H. (1983) Periodic renewal theory. Report, Department of Mathematics, Göteborg.Google Scholar
[21] Williams, D. (1979) Diffusions, Markov Processes, and Martingales. Wiley, Chichester.Google Scholar