Hostname: page-component-55f67697df-gmt7q Total loading time: 0 Render date: 2025-05-09T11:02:49.410Z Has data issue: false hasContentIssue false
  • English
  • Français

Convergence speed and approximation accuracy of numerical MCMC

Part of: Miscellaneous topics - Partial differential equations Probabilistic methods, simulation and stochastic differential equations Ergodic theory

Published online by Cambridge University Press:  02 December 2024

Tiangang Cui ,
Jing Dong ,
Ajay Jasra  and
Xin T. Tong Open the ORCID record for Xin T. Tong [Opens in a new window]
Tiangang Cui*
Affiliation:
University of Sydney
Jing Dong*
Affiliation:
Columbia University
Ajay Jasra*
Affiliation:
The Chinese University of Hong Kong, Shenzhen
Xin T. Tong*
Affiliation:
National University of Singapore
*
*Postal address: School of Mathematics and Statistics, University of Sydney, NSW 2050, Australia. Email: [email protected]
**Postal address: Graduate School of Business, Columbia University, U.S.A. Email: [email protected]
***Postal address: School of Data Science, The Chinese University of Hong Kong, Shenzhen, China. Email: [email protected]
****Postal address: Department of Mathematics, National University of Singapore, Singapore. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

When implementing Markov Chain Monte Carlo (MCMC) algorithms, perturbation caused by numerical errors is sometimes inevitable. This paper studies how the perturbation of MCMC affects the convergence speed and approximation accuracy. Our results show that when the original Markov chain converges to stationarity fast enough and the perturbed transition kernel is a good approximation to the original transition kernel, the corresponding perturbed sampler has fast convergence speed and high approximation accuracy as well. Our convergence analysis is conducted under either the Wasserstein metric or the 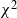$\chi^2$ metric, both are widely used in the literature. The results can be extended to obtain non-asymptotic error bounds for MCMC estimators. We demonstrate how to apply our convergence and approximation results to the analysis of specific sampling algorithms, including Random walk Metropolis, Metropolis adjusted Langevin algorithm with perturbed target densities, and parallel tempering Monte Carlo with perturbed densities. Finally, we present some simple numerical examples to verify our theoretical claims.

Keywords

Bayesian inverse problemsMarkov Chain Monte Carloconvergence speedperturbation analysis

MSC classification

Primary: 35R30: Inverse problems
Secondary: 65C40: Computational Markov chains 37A25: Ergodicity, mixing, rates of mixing
Type
Original Article
Information
Advances in Applied Probability , Volume 57 , Issue 1 , March 2025 , pp. 101 - 133
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Andrieu, C., De Freitas, N., Doucet, A. and Jordan, M. I. (2003). An introduction to MCMC for machine learning. Machine Learning. 50, 5–43.CrossRefGoogle Scholar
Andrieu, C. and Vihola, M. (2015). Convergence properties of pseudo-marginal Markov chain Monte Carlo algorithms. The Annals of Applied Probability. 25, 1030–1077.CrossRefGoogle Scholar
Bakry, D., Gentil, I., Ledoux, M. et al. (2014). Analysis and Geometry of Markov Diffusion Operators, Vol. 103. Springer, Switzerland.CrossRefGoogle Scholar
Bardenet, R., Doucet, A. and Holmes, C. (2014). An adaptive subsampling approach for MCMC inference in large datasets. In Proceedings of The 31st International Conference on Machine Learning.Google Scholar
Beskos, A., Jasra, A., Law, K., Marzouk, Y. and Zhou, Y. (2018). Multilevel sequential Monte Carlo with dimension-independent likelihood-informed proposals. SIAM/ASA Journal on Uncertainty Quantification. 6, 762–786.CrossRefGoogle Scholar
Breyer, L., Roberts, G. O. and Rosenthal, J. S. (2001). A note on geometric ergodicity and floating-point roundoff error. Statistics & Probability Letters 53, 123–127.CrossRefGoogle Scholar
Bui-Thanh, T., Ghattas, O., Martin, J. and Stadler, G. (2013). A computational framework for infinite-dimensional Bayesian inverse problems part i: The linearized case, with application to global seismic inversion. SIAM Journal on Scientific Computing. 35, A2494–A2523.CrossRefGoogle Scholar
Butcher, J. (2016). Numerical Methods for Ordinary Differential Equations. John Wiley & Sons, Hoboken, NJ.CrossRefGoogle Scholar
Chen, X., Du, S. S. and Tong, X. T. (2020). On stationary-point hitting time and ergodicity of stochastic gradient Langevin dynamics. Journal of Machine Learning Research.Google Scholar
Cotter, S. L., Dashti, M. and Stuart, A. M. (2010). Approximation of Bayesian inverse problems for PDEs. SIAM Journal on Numerical Analysis. 48, 322–345.CrossRefGoogle Scholar
Dong, J. and Tong, X. T. (2021). Replica exchange for non-convex optimization. Journal of Machine Learning Research. 22, 1–59.Google Scholar
Dong, J. and Tong, X. T. (2022). Spectral gap of replica exchange Langevin diffusion on mixture distributions. Stochastic Processes and Their Applications. 151, 451–489.CrossRefGoogle Scholar
Dupuis, P., Liu, Y., Plattner, N. and Doll, J. D. (2012). On the infinite swapping limit for parallel tempering. Multiscale Modeling & Simulation. 10, 986–1022.CrossRefGoogle Scholar
Durmus, A. and Moulines, E. (2017). Nonasymptotic convergence analysis for the unadjusted Langevin algorithm. The Annals of Applied Probability. 27, 1551–1587.CrossRefGoogle Scholar
Dwivedi, R., Chen, Y., Wainwright, M. J. and Yu, B. (2018). Log-concave sampling: Metropolis–Hastings algorithms are fast! In Conference on Learning Theory. PMLR. pp. 793–797.Google Scholar
Dwivedi, R., Chen, Y., Wainwright, M. J. and Yu, B. (2019). Log-concave sampling: Metropolis–Hastings algorithms are fast. Journal of Machine Learning Research. 20, 1–42.Google Scholar
Earl, D. J. and Deem, M. W. (2005). Parallel tempering: Theory, applications, and new perspectives. Physical Chemistry Chemical Physics. 7, 3910–3916.CrossRefGoogle ScholarPubMed
Ferré, D., Hervé, L. and Ledoux, J. (2013). Regular perturbation of v-geometrically ergodic Markov chains. Journal of Applied Probability. 50, 184–194.CrossRefGoogle Scholar
Gallegos-Herrada, M. A., Ledvinka, D. and Rosenthal, J. S. (2022). Equivalences of geometric ergodicity of Markov chains. arXiv preprint arXiv:2203.04395.Google Scholar
Hairer, M. and Mattingly, J. C. (2008). Spectral gaps in Wasserstein distances and the 2d stochastic Navier–Stokes equations. The Annals of Probability. 36, 2050–2091.CrossRefGoogle Scholar
Hairer, M., Stuart, A. M. and Vollmer, S. J. (2014). Spectral gaps for a Metropolis–Hastings algorithm in infinite dimensions. The Annals of Applied Probability. 24, 2455–2490.CrossRefGoogle Scholar
Hervé, L. and Ledoux, J. (2014). Approximating Markov chains and v-geometric ergodicity via weak perturbation theory. Stochastic Processes and Their Applications. 124, 613–638.CrossRefGoogle Scholar
Hoang, V. H., Schwab, C. and Stuart, A. M. (2013). Complexity analysis of accelerated MCMC methods for Bayesian inversion. Inverse Problems. 29, 085010.CrossRefGoogle Scholar
Johndrow, J. E. and Mattingly, J. C. (2017). Coupling and decoupling to bound an approximating Markov chain. arXiv preprint arXiv:1706.02040.Google Scholar
Johndrow, J. E. and Mattingly, J. C. (2017). Error bounds for approximations of Markov chains used in Bayesian sampling. arXiv preprint arXiv:1711.05382.Google Scholar
Jones, G. L. (2004). On the Markov chain central limit theorem. Probability Surveys. 1, 299–320.CrossRefGoogle Scholar
Joulin, A. and Ollivier, Y. (2010). Curvature, concentration and error estimates for \Markov chain Monte Carlo. The Annals of Probability. 38, 2418–2442.CrossRefGoogle Scholar
Lindvall, T. (2002). Lectures on the Coupling Method. Courier Corporation, Mineola, NY.Google Scholar
Lotka, A. J. (1925). Elements of Physical Biology. Williams & Wilkins, Baltimore, MD.Google Scholar
Medina-Aguayo, F., Rudolf, D. and Schweizer, N. (2020). Perturbation bounds for Monte Carlo within Metropolis via restricted approximations. Stochastic Processes and Their Applications. 130, 2200–2227.CrossRefGoogle ScholarPubMed
Meyn, S. P. and Tweedie, R. L. (2012). Markov Chains and Stochastic Stability. Springer Science & Business Media, London.Google Scholar
Negrea, J. and Rosenthal, J. S. (2021). Approximations of geometrically ergodic reversible Markov chains. Advances in Applied Probability. 53, 981–1022.CrossRefGoogle Scholar
Parno, M. D. and Marzouk, Y. M. (2018). Transport map accelerated Markov chain Monte Carlo. SIAM/ASA Journal on Uncertainty Quantification. 6, 645–682.CrossRefGoogle Scholar
Pillai, N. S. and Smith, A. (2014). Ergodicity of approximate MCMC chains with applications to large data sets. arXiv preprint arXiv:1405.0182.Google Scholar
Roberts, G. O., Rosenthal, J. S. and Schwartz, P. O. (1998). Convergence properties of perturbed Markov chains. Journal of Applied Probability. 35, 1–11.CrossRefGoogle Scholar
Roberts, G. O. and Tweedie, R. L. (1996). Exponential convergence of Langevin distributions and their discrete approximations. Bernoulli. 2, 341–363.CrossRefGoogle Scholar
Rudolf, D. (2012). Explicit error bounds for Markov chain Monte Carlo. Dissertationes Math. 485, 1–93.CrossRefGoogle Scholar
Rudolf, D. and Schweizer, N. (2018). Perturbation theory for markov chains via wasserstein distance. Bernoulli 24, 2610–2639.CrossRefGoogle Scholar
Shardlow, T. and Stuart, A. M. (2000). A perturbation theory for ergodic Markov chains and application to numerical approximations. SIAM Journal on Numerical Analysis. 37, 1120–1137.CrossRefGoogle Scholar
Stuart, A. M. (2010). Inverse problems: A Bayesian perspective. Acta Numerica. 19, 451–559.CrossRefGoogle Scholar
Sugita, Y. and Okamoto, Y. (1999). Replica-exchange molecular dynamics method for protein folding. Chemical Physics Letters. 314, 141–151.CrossRefGoogle Scholar
Tawn, N. G. and Roberts, G. O. (2019). Accelerating parallel tempering: Quantile tempering algorithm (quanta). Advances in Applied Probability. 51, 802–834.CrossRefGoogle Scholar
Tawn, N. G., Roberts, G. O. and Rosenthal, J. S. (2020). Weight-preserving simulated tempering. Statistics and Computing. 30, 27–41.CrossRefGoogle Scholar
Tierney, L. (1994). Markov chains for exploring posterior distributions. The Annals of Statistics. 1701–1728.Google Scholar
Vempala, S. and Wibisono, A. (2019). Rapid convergence of the unadjusted Langevin algorithm: Isoperimetry suffices. Advances in Neural Information Processing Systems. 32.Google Scholar
Woodard, D. B., Schmidler, S. C. and Huber, M. (2009). Conditions for rapid mixing of parallel and simulated tempering on multimodal distributions. The Annals of Applied Probability. 19, 617–640.CrossRefGoogle Scholar