Published online by Cambridge University Press: 23 September 2022
In this paper we estimate the expected error of a stochastic approximation algorithm where the maximum of a function is found using finite differences of a stochastic representation of that function. An error estimate of the order
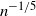 $n^{-1/5}$
for the nth iteration is achieved using suitable parameters. The novelty with respect to previous studies is that we allow the stochastic representation to be discontinuous and to consist of possibly dependent random variables (satisfying a mixing condition).
$n^{-1/5}$
for the nth iteration is achieved using suitable parameters. The novelty with respect to previous studies is that we allow the stochastic representation to be discontinuous and to consist of possibly dependent random variables (satisfying a mixing condition).