Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-07T14:29:00.154Z Has data issue: false hasContentIssue false
  • English
  • Français

A class of branching processes on a lattice with interactions

Published online by Cambridge University Press:  01 July 2016

Klaus Schürger
Klaus Schürger*
Affiliation:
German Cancer Research Centre
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, a very general class of branching processes on the d-dimensional square lattice is studied. It is assumed that the division rates as well as the spatial distribution of offspring are configuration-dependent. The main interest of this paper is in the asymptotic geometrical behaviour of such processes. Utilizing techniques mainly due to Richardson [28], we derive conditions which are necessary and sufficient for such branching processes to have the following property: there exists a norm N(·) on Rd such that, for all 0 < ∊ < 1, we have that almost surely for all sufficiently large t, all sites in the N-ball of radius (1 – ∊)t are contained in 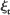(the set of sites occupied at time t) and 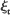is contained in the set of all sites in the N-ball of radius (1 + ∊)t (given that the process starts with finitely many particles).

Keywords

SPATIAL SPREAD PROCESSBRANCHING PROCESS WITH INTERACTIONSTUMOUR GROWTHEDEN PROCESSSTRONG LAW OF LARGE NUMBERSCORRELATION INEQUALITY
Type
Research Article
Information
Advances in Applied Probability , Volume 13 , Issue 1 , March 1981 , pp. 14 - 39
Copyright
Copyright © Applied Probability Trust 1981 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Biggins, J. D. (1978) The asymptotic shape of the branching random walk. Adv. Appl. Prob. 10, 62–84.Google Scholar
[2] Biggins, J. D. (1979) Spatial spread in branching processes. Submitted for publication.Google Scholar
[3] Blumenthal, R. M. and Getoor, R. K. (1968) Markov Processes and Potential Theory. Academic Press, New York.Google Scholar
[4] Bramson, M. and Griffeath, D. (1979) On the Williams–Bjerknes tumour growth model. I. Ann. Prob. To appear.Google Scholar
[5] Bramson, M. and Griffeath, D. (1979) On the Williams–Bjerknes tumour growth model. II. Math. Proc. Camb. Phil. Soc. To appear.Google Scholar
[6] Clifford, P. and Sudbury, A. (1973) A model for spatial conflict. Biometrika 60, 581–588.Google Scholar
[7] Cox, J. T. and Durrett, R. (1979) Some limit theorems for percolation processes with necessary and sufficient conditions. Ann. Prob. To appear.Google Scholar
[8] Dieudonné, J. (1970) Treatise on Analysis, Vol. 2. Academic Press, New York.Google Scholar
[9] Dunford, N. and Schwartz, J. T. (1964) Linear Operators. I: General Theory. Interscience, New York.Google Scholar
[10] Dynkin, E. B. (1965) Markov Processes, Vol. 1. Springer-Verlag, Berlin.Google Scholar
[11] Eden, M. (1961) A two-dimensional growth process. Proc. 4th Berkeley Symp. Math. Statist. Prob. 4, 223–239.Google Scholar
[12] Gray, L. and Griffeath, D. (1977) On the uniqueness and nonuniqueness of proximity processes. Ann. Prob. 5, 678–692.Google Scholar
[13] Griffeath, D. (1979) Additive and Cancellative Interacting Particle Systems. Lecture Notes in Mathematics 724, Springer-Verlag, Berlin.Google Scholar
[14] Hammersley, J. M. (1962) Generalization of the fundamental theorem on subadditive functions. Proc. Camb. Phil. Soc. 58, 235–238.Google Scholar
[15] Hammersley, J. M. (1966) First-passage percolation. J. R. Statist. Soc. B 28, 491–496.Google Scholar
[16] Hammersley, J. M. (1974) Postulates for subadditive processes. Ann. Prob. 2, 652–680.Google Scholar
[17] Harris, T. E. (1974) Contact interactions on a lattice. Ann. Prob. 2, 969–988.Google Scholar
[18] Harris, T. E. (1977) A correlation inequality for Markov processes in partially ordered state spaces. Ann. Prob. 5, 451–454.CrossRefGoogle Scholar
[19] Holley, R. A. and Liggett, T. M. (1975) Ergodic theorems for weakly interacting infinite systems and the voter model. Ann. Prob. 3, 643–663.CrossRefGoogle Scholar
[20] Kelly, F. P. (1977) The asymptotic behaviour of an invasion process. J. Appl. Prob. 14, 584–590.Google Scholar
[21] Kesten, H. (1973) Contribution to the discussion in [22], p. 903.Google Scholar
[22] Kingman, J. F. C. (1973) Subadditive ergodic theory. Ann. Prob. 1, 883–909.CrossRefGoogle Scholar
[23] Kurtz, T. G. (1969) Extensions of Trotter's operator semigroup approximation theorems. J. Functional Anal. 3, 354–375.Google Scholar
[24] Liggett, T. M. (1972) Existence theorems for infinite particle systems. Trans. Amer. Math. Soc. 165, 471–481.Google Scholar
[25] Liggett, T. M. (1977) The stochastic evolution of infinite systems of interacting particles. In Lecture Notes in Mathematics 598, Springer-Verlag, Berlin, 187–248.Google Scholar
[26] Loève, M. (1963) Probability Theory 3rd edn. Van Nostrand, Princeton, N.J. Google Scholar
[27] Lumer, G. and Phillips, R. S. (1961) Dissipative operators in a Banach space. Pacific J. Math. 11, 679–698.CrossRefGoogle Scholar
[28] Richardson, D. (1973) Random growth in a tessellation. Proc. Camb. Phil. Soc. 74, 515–528.CrossRefGoogle Scholar
[29] Schürger, K. (1979) On the asymptotic geometrical behaviour of a class of contact interaction processes with a monotone infection rate. Z. Wahrscheinlichkeitsth. 48, 35–48.Google Scholar
[30] Schürger, K. (1980) On the asymptotic geometrical behaviour of percolation processes. J. Appl. Prob. 17, 385–402.CrossRefGoogle Scholar
[31] Schürger, K. and Tautu, P. (1976) A Markovian configuration model for carcinogenesis. In Mathematical Models in Medicine. Lecture Notes in Biomathematics 11, Springer-Verlag, Berlin, 92–108.CrossRefGoogle Scholar
[32] Schwartz, D. (1977) Applications of duality to a class of Markov processes. Ann. Prob. 5, 522–532.Google Scholar
[33] Schwöbel, W., Geidel, H. and Lorenz, R. J. (1966) Ein Modell der Plaquebildung. Z. Naturforsch. 21, 953–959.Google Scholar
[34] Smythe, R. T. and Wierman, J. C. (1978) First-Passage Percolation on the Square Lattice. Lecture Notes in Mathematics 671, Springer-Verlag, Berlin.Google Scholar
[35] Sudbury, A. (1976) The size of the region occupied by one type in an invasion process. J. Appl. Prob. 13, 355–356.Google Scholar
[36] Sullivan, W. G. (1975) Markov Processes for Random Fields. Comm. Dublin Inst. Adv. Studies Ser. A, No. 23.Google Scholar
[37] Williams, T. and Bjerknes, R. (1971) Hyperplasia: the spread of abnormal cells through a plane lattice. Adv. Appl. Prob. 3, 210–211.Google Scholar
[38] Williams, T. and Bjerknes, R. (1972) Stochastic model for abnormal clone spread through epithelial basal layer. Nature (London) 236, 19–21.Google Scholar