No CrossRef data available.
Article contents
A central limit theorem for jump diffusion processes in the presence of round-off errors
Part of:
Limit theorems
Published online by Cambridge University Press: 25 March 2025
Abstract
Let X be the sum of a diffusion process and a Lévy jump process, and for any integer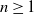 
$n\ge 1$ let 
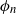$\phi_n$ be a function defined on 
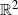$\mathbb{R}^2$ and taking values in 
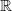$\mathbb{R}$, with adequate properties. We study the convergence of functionals of the type where [x] is the integer part of the real number x and the sequences 
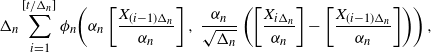\begin{align*} \Delta_n\sum_{i=1}^{[t/\Delta_n]} \phi_n\!\left(\alpha_n\left[\frac{X_{(i-1)\Delta_n}}{\alpha_n}\right], \:\frac{\alpha_n}{\sqrt{\Delta_n}}\left(\left[\frac{X_{i\Delta_n}}{\alpha_n}\right]-\left[\frac{X_{(i-1)\Delta_n}}{\alpha_n}\right]\right)\right),\end{align*}
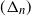$(\Delta_n)$ and 
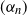$(\alpha_n)$ tend to 0 as 
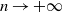$n\to +\infty$. We then prove the law of large numbers and establish, in the case where 
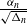$\frac{\alpha_n}{\sqrt{\Delta_n}}$ converges to a real number in 
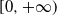$[0,+\infty)$], a new central limit theorem which generalizes that in the case where X is a continuous Itô’s semimartingale.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of Applied Probability Trust
References
At-Sahalia, Y. and Jacod, J. (2009): Testing for jumps is a discretely observed process. Ann. Statist. 37 (1), 184–222.Google Scholar
At-Sahalia, Y. and Jacod, J. (2009): Estimating the degree of activity of jumps in high frequency data. Ann. Statist. 37 (5A), 2202–2244.Google Scholar
At-Sahalia, Y. and Jacod, J. (2011): Testing whether jumps have finite or infinite activity. Ann. Statist. 39 (3), 1689–1719.Google Scholar
Barndorff-Nielsen, O.E. and Shephard, N. (2003). Realized power variation and stochastic volatility models. Bernoulli 9 243–265. MR1997029Google Scholar
Cumenge, Pierre-Henri. (2011): p-Variations approchées et erreurs d’arrondis. Thèse de Doctorat Université de Paris 6.Google Scholar
Delattre, S. and Jacod, J. (1997): A central limit theorem for normalized functions of the increments of a diffusion processes, in the presence of round-off errors. Bernoulli, 3(1), 1997, 1-28.CrossRefGoogle Scholar
Delattre, S. (1997): Estimation du coefficient de diffusion d’un processus de diffusion en présences d’erreurs d’arrondi. Thèse de Doctorat Université de Paris 6.Google Scholar
Diop, A. (2012). Convergences of some random functionals of discretized semimartingales. Bernoulli 18 (4) 1188–1222.Google Scholar
Jacod, J., Protter, P. (2012): Discretization of processes. Stochastic Modelling and Applied Probability 67. SpringerCrossRefGoogle Scholar
Jacod, J. (2007): Asymptotic properties of realized power variations and related functionals of semimartingale. Stochastics Process. Appl. 118 517–559. MR2394762Google Scholar
Jacod, J. (2003): Asymptotic properties of power variations of Lévy processes. ESAIM Probab. Stat. 11 173–196. MR2320818Google Scholar
Jacod, J., Shiryaev, A. N. (2002):Limit theorems for stochastic processes. Springer, Volume 288, Second edition.Google Scholar
Jacod, J. (1996): La variation quadratique du brownien en présence d’erreurs d’arrondis. Astérisque, 236, 155–161.Google Scholar
Genon-Catalot, V. Jacod, J. (1993): On the estimation of the diffusion coefficient for multidimensional diffusion processes. Ann. Inst. H. Poincaré. Probab. Stat., 29, 119-151.Google Scholar
Rosenbaum, M. (2009): Integrated volatility and round-off error. Bernoulli, 15(3): 687–720.Google Scholar
Wilms, R. J. G. (1994): Fractional parts of random variables : limit theorems and infinite divisibility. Eindhoven: Technische Universiteit Eindhoven DOI: 10.6100/IR423641
Google Scholar