Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-09T06:52:01.627Z Has data issue: false hasContentIssue false
  • English
  • Français

The branching property in generalized information theory

Published online by Cambridge University Press:  01 July 2016

Bruce Ebanks
Bruce Ebanks*
Affiliation:
Texas Tech University
Get access Rights & Permissions [Opens in a new window]

Abstract

It is shown that every measure of expected information which has the branching property is of the form 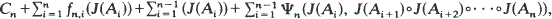where J is a given information measure which is compositive under a regular binary operation 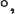and the Ψn are antisymmetric, bi-additive functions. In a probability space, such measures (entropies) take the form

Keywords

INFORMATION MEASURECOMPOSITIVEREGULAR BINARY OPERATIONORDERED TOPOLOGICAL SEMIGROUPENTROPYBRANCHING PROPERTYPROBABILITY SPACE
Type
Research Article
Information
Advances in Applied Probability , Volume 10 , Issue 4 , December 1978 , pp. 788 - 802
Copyright
Copyright © Applied Probability Trust 1978 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aczél, J. and Daróczy, Z. (1975) On Measures of Information and their Characterizations. Academic Press, New York.Google Scholar
Forte, B. (1976) A characterization of the entropy functionals for grand canonical ensembles. The discrete case. Ann. Mat. Pura Appl. (4) 111, 213–228.CrossRefGoogle Scholar
Forte, B. and Bortone, C. A. (1977) Non-symmetric entropies with the branching property. Utilitas Math. 12, 3–23.Google Scholar
Forte, B. and Ng, C. T. (1974) Entropies with the branching property. Ann. Mat. Pura Appl. (4) 101, 355–373.Google Scholar
Kampé de Fériet, J. and Forte, B. (1967) Information et probabilité. C.R. Acad. Sci. Paris 265, 110–114.Google Scholar
Kampé de Fériet, J., Forte, B. and Benvenuti, P. (1969) Forme générale de l'opération de composition continue d'une information. C.R. Acad. Sci. Paris 269, 529–534.Google Scholar
Mostert, P. S. and Shields, A. L. (1957) On the structure of semigroups on a compact manifold with boundary Ann. Math. 65, 117–143.Google Scholar