Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T02:58:41.284Z Has data issue: false hasContentIssue false
  • English
  • Français

Blocking probabilities for large multirate erlang loss systems

Part of: Special processes Operations research and management science

Published online by Cambridge University Press:  01 July 2016

Pawel Gazdzicki ,
Ioannis Lambadaris  and
Ravi R. Mazumdar
Pawel Gazdzicki
Affiliation:
Université du Québec
Ioannis Lambadaris*
Affiliation:
Concordia University
Ravi R. Mazumdar*
Affiliation:
Université du Quebec
*
** Postal address: Department of Electrical Engineering, Concordia University, Montreal, P.Q. H3G 1M8, Canada.
* Postal address: INRS-Télécommunications, Université du Québec, Ile des Soeurs, P.Q. H3E 1H6, Canada.
Get access Rights & Permissions [Opens in a new window]

Abstract

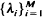This paper is concerned with the computation of asymptotic blocking probabilities for a generalized Erlangian system which results when M independent Poisson streams of traffic with rates access a trunk group of C circuits with traffic from stream k requiring Ak circuits which are simultaneously held and released after a time which is randomly distributed with unit mean and independent of earlier arrivals and holding times. A call from stream k is lost if on arrival less than Ak circuits are available. Although exact expressions for the blocking probabilities are known, their computation is unwieldy for even moderate-sized switches. It is shown that as the size of the switch increases in that both the traffic rates and trunk capacity are scaled together, simple asymptotic expressions for the blocking probabilities are obtained. In particular the expression is different for light, moderate and heavy loads. The approach is via exponential centering and large deviations and provides a unified framework for the analysis.

Keywords

EXPONENTIAL CENTERINGLARGE DEVIATIONSLOCAL LIMIT THEOREMS

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 60K30: Applications (congestion, allocation, storage, traffic, etc.) 60K25: Queueing theory 90B15: Network models, stochastic
Type
Research Article
Information
Advances in Applied Probability , Volume 25 , Issue 4 , December 1993 , pp. 997 - 1009
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Bahadur, R. R. and Ranga Rao, R. (1960) On deviations of the sample mean. Ann. Math. Statist. 31, 1015–1027.CrossRefGoogle Scholar
[2] Bucklew, J. A. (1990) Large Deviations Techniques in Decision, Simulation and Estimation. Wiley, New York.Google Scholar
[3] Dziong, Z. and Roberts, J. W. (1987) Congestion probabilities in a circuit-switched integrated services network. Performance Eval. 7, 267–284.Google Scholar
[4] Gnedenko, B. (1976) The Theory of Probability, English translation. Mir, Moscow.Google Scholar
[5] Hunt, P. J. and Kelly, F. P. (1989) On critically loaded loss networks. Adv. Appl. Prob. 21, 831–841.Google Scholar
[6] Kaufman, J. S. (1981) Blocking in a shared resources environment. IEEE Trans. Comm. 29, 1474–1481.CrossRefGoogle Scholar
[7] Kelly, F. P. (1986) Blocking probabilities in large circuit switched networks. Adv. Appl. Prob. 18, 473–505.Google Scholar
[8] Kelly, F. P. (1991) Loss networks. Ann. Appl. Prob. 1, 319–378.Google Scholar
[9] Mckenna, J. and Mitra, D. (1982) Integral representations and asymptotic expansions for closed Markovian queueing systems–normal usage. Bell System Tech. J., 61, 661–683.Google Scholar
[10] Petrov, V. V. (1975) Sums of Independent Random Variables, translated by Brown, A. A. Springer-Verlag, Berlin.Google Scholar
[11] Reiman, M. I. (1991) A critically loaded multiclass Erlang loss system. QUESTA 9, 65–82.Google Scholar
[12] Simonian, A. (1992) Analyse asymptotique des taux de blocage pour un traffic multidébit. Ann. Télécomm. 47, 56–63.CrossRefGoogle Scholar
[13] Varadhan, S. R. S. (1984) Large Deviations and Applications. SIAM, Philadelphia.CrossRefGoogle Scholar