Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-06T08:09:30.634Z Has data issue: false hasContentIssue false
  • English
  • Français

The biased annihilating branching process

Part of: Special processes

Published online by Cambridge University Press:  01 July 2016

Claudia Neuhauser  and
Aidan Sudbury
Claudia Neuhauser*
Affiliation:
University of Southern California
Aidan Sudbury*
Affiliation:
Monash University
*
∗Postal address: Department of Mathematics, University of Southern California, Los Angeles, CA 90089-1113, USA. Partially supported by the National Science Foundation.
∗∗Postal address: Mathematics Department, Monash University, Clayton, VIC 3168, Australia.
Get access Rights & Permissions [Opens in a new window]

Abstract

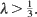In the biased annihilating branching process, particles place offspring on empty neighboring sites at rate A and destroy neighbors at rate 1. It is conjectured that for any λ ≥ 0 the population will spread to ∞, and this is shown in one dimension for The process on a finite graph when starting with a non-empty configuration has limiting distribution vλ /(λ +1), the product measure with density λ/(1 +λ). It is shown that vλ /(λ +1) and δ Ø are the only stationary distributions on Moreover, if 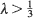and the initial configuration is non-empty, then the limiting measure is vλ /(λ +1) provided the initial measure converges.

Keywords

INFINITE PARTICLE SYSTEMANNIHILATION

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Type
Research Article
Information
Advances in Applied Probability , Volume 25 , Issue 1 , March 1993 , pp. 24 - 38
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bramson, M. and Gray, L. (1985) The survival of the branching annihilating random walk. Z. Wahrscheinlichkeitsth. 68, 447–460.CrossRefGoogle Scholar
Bramson, M., Ding, W. D. and Durrett, R. (1991) Annihilating branching processes. Stoch. Proc. Appl. 27, 1–18.Google Scholar
Ding, W. D., Durrett, R. and Liggett, T. (1990) Ergodicity of reversible reaction diffusion processes. Prob. Theory Rel. Fields 85, 13–26.Google Scholar
Harris, T. E. (1974) Contact interactions on a lattice. Ann. Prob. 2, 969–988.Google Scholar
Liggett, T. M. (1977) The stochastic evolution of infinite systems of interacting particle systems. Ecole d'Eté de Probabilité de Saint-Flour VI, 1976. Springer Lecture Notes in Mathematics 598, 187–248.Google Scholar
Liggett, T. M. (1985) Interacting Particle Systems. Springer-Verlag, New York.CrossRefGoogle Scholar
Sudbury, A. W. (1989a) The branching annihilating process with non-nearest neighbour interactions. Monash University Research Report No. 194.Google Scholar
Sudbury, A. W. (1989b) Geometric bounds for a particle moving under different random walk regimes. Preprint.Google Scholar
Sudbury, A. W. (1990) The branching annihilating process: an interacting particle system. Ann. Prob. 18, 581–601.Google Scholar
Yaguchi, H. (1990) Entropy analysis of a nearest neighbor attractive/repulsive exclusion process on one-dimensional lattices. Ann. Prob. 18, 556–580.Google Scholar
Ziezold, H. and Grillenberger, C. (1988) On the critical infection rate of the one-dimensional basic contact process: numerical results. J. Appl. Prob. 25, 1–8.Google Scholar